Базис и координаты в n-мерном пространстве
Совокупность каких-либо n линейно независимых векторов 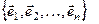 называются базисом n-мерного пространства.
называются базисом n-мерного пространства.
Любой вектор 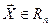 может быть представлен в виде линейной комбинации базисных векторов
может быть представлен в виде линейной комбинации базисных векторов 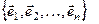 , т.е. существуют такие числа хi, i=1,…,n, что
, т.е. существуют такие числа хi, i=1,…,n, что
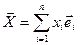 .
.
Числа xi называются координатами вектора 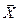 в базисе
в базисе 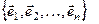 .
.
Используя частный случай единичных базисных векторов
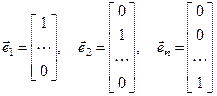
можно любой набор n чисел (x1, x2 …xn) представить вектором 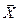 линейного пространства Rn, причем числа xi являются координатами этого вектора в базисе единичных векторов
линейного пространства Rn, причем числа xi являются координатами этого вектора в базисе единичных векторов 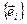 .
. 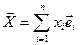 Если при этом
Если при этом 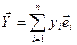 , то
, то
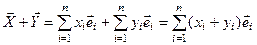 ,
,
т.е. координаты суммы векторов равны сумме соответствующих координат.
Понятие базиса и координат вектора Х произвольной природы в базисе 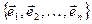 позволяет свести вектора любого характера к векторам, представляющим собой систему n чисел. Например, многочлены
позволяет свести вектора любого характера к векторам, представляющим собой систему n чисел. Например, многочлены
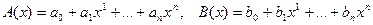
можно представить через базис
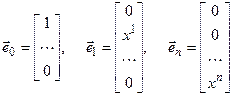 ,
,
в котором 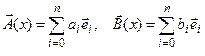 , т.е. множество полиномов степениn представляется как линейное пространство Rn+1. Этот результат справедлив для любых векторов и в общем виде сводится к алгебраической неразличимости (изоморфизму) векторов любой природы, но одинаковой размерности.
, т.е. множество полиномов степениn представляется как линейное пространство Rn+1. Этот результат справедлив для любых векторов и в общем виде сводится к алгебраической неразличимости (изоморфизму) векторов любой природы, но одинаковой размерности.
Дата добавления: 2020-07-18; просмотров: 749;











