Сложение поступательных движений НМС

Сложное движение НМС

Абсолютное, относительное и переносное

Движения НМС

Определение: Движение НМС, рассматриваемое одновременно относительно нескольких систем координат, хотя бы одна из которых неподвижна, называется сложным движением.

Иначе говоря, сложным движением НМС называется такое движение НМС, которое может рассматриваться состоящим из нескольких движений.

При рассмотрении сложного движения НМС, как и в случае сложного движения МТ (глава 7), оказывается удобным классифицировать движения НМС на абсолютное, относительное и переносное, введя аналогичным способом неподвижную и подвижную системы координат.

Определение: Абсолютным движением НМС называется движение НМС относительно неподвижной системы координат.

Определение: Относительным движением НМС называется движение НМС относительно подвижной системы координат.

Определение: Переносным движением НМС называется движение НМС вместе с подвижной системой координат относительно неподвижной системы координат.

В данной главе рассматриваются способы нахождения для данного момента времени распределения скоростей МТ, принадлежащих НМС, соответствующие сложному движению НМС при различных частных случаях относительного и переносного движений НМС.

В кинематике сложного движения НМС также решаются две задачи: "сложения" и "разложения", аналогичные тем, которые решались в кинематике сложного движения МТ.

Сложение поступательных движений НМС

Пусть НМС движется поступательно со скоростью 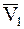по отношению к подвижной системе координат Oxyz, которая, в свою очередь, движется поступательно со скоростью 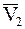по отношению к неподвижной системе координат O₁xhz (рис. 79).

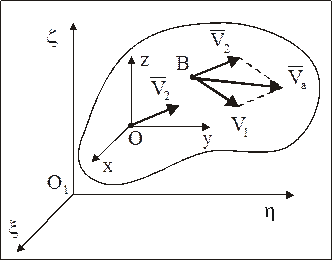
Рис. 79

Так как относительное движение НМС — поступательное, то относительные скорости 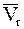всех МТ, принадлежащих НМС, одинаковы и равны 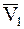, т. е. = .

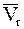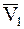Так как переносное движение НМС — поступательное, то переносные скорости 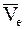всех МТ, принадлежащих НМС, одинаковы и равны 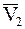, т. е. = .

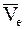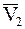На основании теоремы о сложении скоростей МТ в сложном движении (7.8) абсолютная скорость 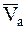любой МТ, принадлежащих НМС, в какой-либо момент времени определяется формулой:

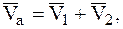(8.1)

т. е. абсолютные скорости всех МТ, принадлежащих НМС, равны между собой.

Если НМС одновременно совершает n поступательных движений со скоростями 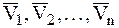, то, применяя последовательно формулу (8.1), получим:

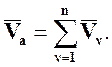(8.2)

При сложении нескольких поступательных движений НМС ее абсолютное движение будет поступательным, причём скорость этого поступательного движения (следовательно, и скорости всех ее МТ) будет равна геометрической сумме скоростей этих нескольких поступательных движений.