Вокруг пересекающихся осей

Пусть НМС вращается вокруг оси Oz с угловой скоростью 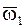, а ось Oz, в свою очередь, вращается вместе с НМС вокруг пересекающейся с ней в точке О оси Оz неподвижной системы координат Oxhz с угловой скоростью 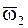(рис. 80).

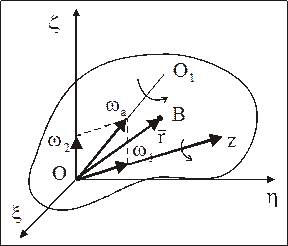
Рис. 80

Вращательное движение НМС вокруг подвижной оси Oz – относительное движение НМС, а вращательное движение самой оси Oz вместе с НМС вокруг неподвижной оси Оz – переносное движение.

Точка О, в которой пересекаются оси Oz и Оz, остается при движении НМС неподвижной, т. е. это сложное движение НМС эквивалентно движению НМС с одной неподвижной точкой и абсолютное движение НМС может быть представлено как мгновенное вращательное движение НМС с угловой скоростью 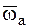вокруг мгновенной оси ОO₁, проходящей через точку О.

Чтобы определить 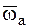, найдем на основании формулы (7.8) абсолютную скорость МТ, принадлежащей НМС, радиус-вектор которой 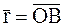(рис. 80):

.

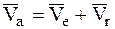Так как вращательные скорости абсолютного, относительного и переносного движения МТ определяются формулой (3.13), то

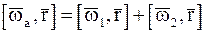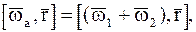или т. е.

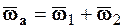. (8.3)

Если НМС участвует в нескольких вращениях вокруг нескольких осей, пересекающихся в точке О, то, последовательно применяя формулу (8.3), найдем, что абсолютное движение НМС будет мгновенным вращательным движением вокруг мгновенной оси, проходящей через точку О с угловой скоростью:

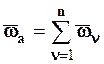. (8.4)

При сложении вращений НМС вокруг нескольких осей, пересекающихся в одной точке О, абсолютное движение НМС будет мгновенным вращательным вокруг оси ОO₁, проходящей через точку О, а угловая скорость этого вращения будет равна геометрической сумме составляющих угловых скоростей. Мгновенная ось вращения ОO₁ направлена вдоль вектора 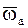(в случае сложения двух вращений мгновенная ось вращения направлена по диагонали параллелограмма, построенного на векторах 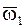и 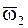(рис. 80)). Мгновенная ось вращения с течением времени меняет свое положение, описывая коническую поверхность с вершиной в точке О.