ПРОСТЕЙШИЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА

I. Постоянный множитель 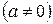можно выносить за знак интеграла:

.

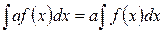II. Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от слагаемых функций:

.

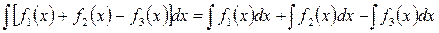III. Производная от неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению

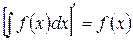или .

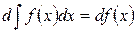IV. Неопределенный интеграл от дифференциала функции равен сумме этой функции и произвольной 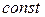, т.е.

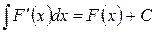или .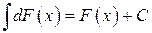

V. Если справедливо равенство 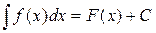, то справедливым будет и соотношение:

.

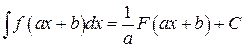ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ

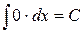
	(1)
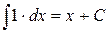
	(2)
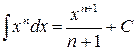
	(3)
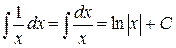
	(4)
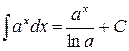
	(5)
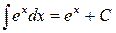
	(6)
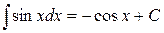
	(7)
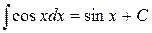
	(8)
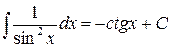
	(9)
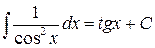
	(10)
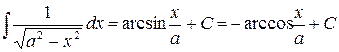
	(11)
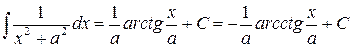
	(12)
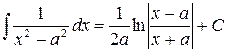
	(13)
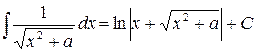
	(14)
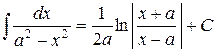
	(15)

Справедливость формул можно проверить путем дифференцирования, т.е. надо убедиться в том, что производные от правых частей формул будут равны соответственно подынтегральным функциям. Так, если 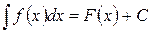, то .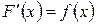

Например, в формуле (14) ; ;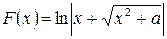

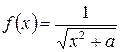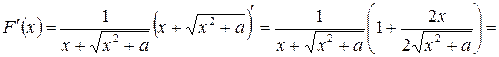
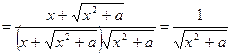, т.е. .

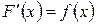Аналогичным способом можно проверить и все остальные формулы. Заметим, что каждая из формул таблицы справедлива в любом промежутке, содержащемся в области определения подынтегральной функции.

Интегралы таблицы называются табличными