ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.

В дифференциальном исчислении одной из основных задач является нахождение производной или дифференциала от данной функции :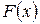

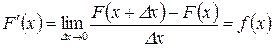
Или .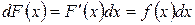

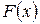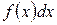В интегральном исчислении основной является обратная задача – отыскание функции по заданной ее производной или дифференциалу , т.е. для данной функции надо найти такую функцию 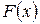, что

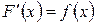
или

.

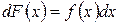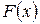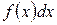Функция , производная которой равна , а дифференциал называется первообразной функцией для функции .

Приведем примеры.

1) Если 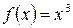, то первообразная будет 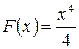, так как .

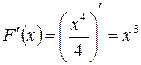2) Если 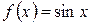, то 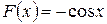, так как .

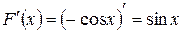Заметим, что если 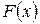– первообразная функция для функции 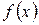, то и 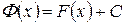( 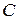–произвольная постоянная) есть также первообразная функция, так как

.

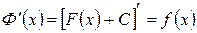Например, пусть 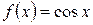, тогда 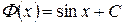будет первообразной функцией для данной функции 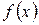, так как

.

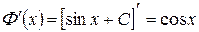Общее выражение 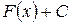совокупности всех первообразных функций для данной непрерывной функции 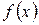называется неопределенным интегралом от функции 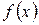и обозначается символом 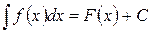, где 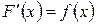. Функция 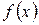называется подынтегральной функцией, 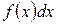– подынтегральным выражением.

Задача состоит в нахождении хотя бы одной первообразной, что достигается путем интегрирования. При этом следует иметь в виду, что правильность интегрирования проверяется дифференцированием.