Производная функции
Таблица производных
Логарифмическая производная
Производная сложной функции
Производная высших порядков
Производная функции
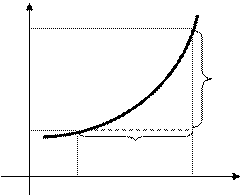
Рассмотрим функцию 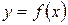 . Пусть
. Пусть  – некоторое значение аргумента,
– некоторое значение аргумента,  – соответствующее значение функции. От значения
– соответствующее значение функции. От значения  переходим к другому значению аргумента
переходим к другому значению аргумента 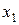 . Разность
. Разность 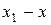 (обозначим через
(обозначим через 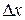 ) называется приращением аргумента. Значение функции, соответствующее значению аргумента
) называется приращением аргумента. Значение функции, соответствующее значению аргумента 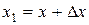 , равно
, равно 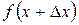 . Разность
. Разность 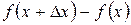 называется приращением функции
называется приращением функции 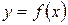 в точке
в точке  , соответствующим приращению аргумента
, соответствующим приращению аргумента 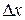 , и обозначается
, и обозначается 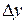 или
или 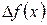 :
:
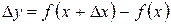 (2.1.1)
(2.1.1)
| 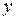
| ||||||||||||||||
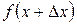
| |||||||||||||||||
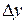
| |||||||||||||||||
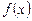
| |||||||||||||||||
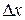
| |||||||||||||||||

| 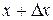
| 
| |||||||||||||||
Рисунок 2.1 – Геометрическая интерпретация приращения функции
Производнойфункции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента (т.е.
называется предел отношения приращения функции к приращению аргумента (т.е. 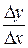 ) при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
) при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
Производная функции 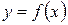 в точке
в точке  обозначается символами
обозначается символами 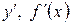 или
или 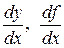 . Т.о., по определению
. Т.о., по определению
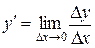 (2.1.2)
(2.1.2)
Таблица производных
1. 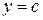 ; ;
| 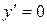 ; ;
| 10. 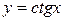 ; ;
| 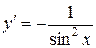 ; ;
|
2. 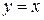 ; ;
| 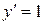 ; ;
| 11. 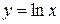 ; ;
| 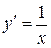 ; ;
|
3. 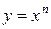 ; ;
| 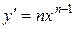 ; ;
| 12. 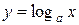 ; ;
| 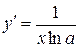 ; ;
|
4. 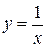 ; ;
| 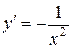 ; ;
| 13. 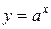 ; ;
| 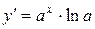 ; ;
|
5. 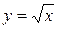 ; ;
| 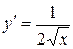 ; ;
| 14. 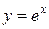 ; ;
| 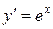 ; ;
|
6. 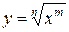 ; ;
| 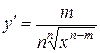 ; ;
| 15. 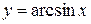 ; ;
| 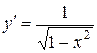 ; ;
|
7. 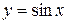 ; ;
| 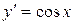 ; ;
| 16. 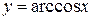 ; ;
|  ; ;
|
8. 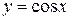 ; ;
| 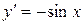 ; ;
| 17. 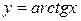 ; ;
| 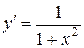 ; ;
|
9. 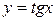 ; ;
| 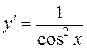 ; ;
| 18. 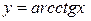 ; ;
| 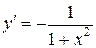 . .
|
Пример.Найти производную функции 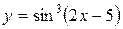
Решение.Полагая 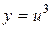 ,
, 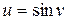 ;
; 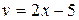 ; получим
; получим
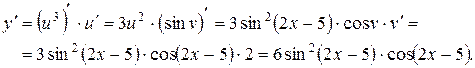
При достаточном количестве упражнений необходимость в записи промежуточных переменных отпадает.
Если функция задана неявно, т.е. уравнением, не разрешенным относительно 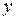 (
( 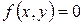 ), то для нахождения производной
), то для нахождения производной 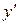 надо продифференцировать по
надо продифференцировать по  обе части этого уравнения, учитывая, что
обе части этого уравнения, учитывая, что 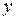 есть функция от
есть функция от  , и затем разрешить полученное уравнение относительно
, и затем разрешить полученное уравнение относительно 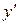 .
.
Пример.Найти производную функции 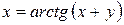 .
.
Решение.Дифференцируем по  обе части данного равенства и считаем
обе части данного равенства и считаем 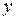 функцией от
функцией от  , находим
, находим
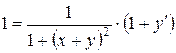 .
.
Из полученного равенства находим 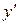 .
.
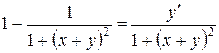 ;
;
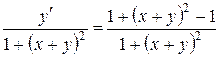 ;
;
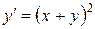 .
.
Логарифмическая производная функции 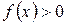 есть производная от логарифма данной функции:
есть производная от логарифма данной функции:
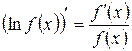 .
.
4.3. Логарифмическое дифференцирование.
Вычисление логарифмической производной называется логарифмическим дифференцированием.
Логарифмическое дифференцирование применяется при вычислении производной степенно-показательной функции, т.е. функции вида 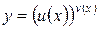 , а также при нахождении производной произведения нескольких функций или производной дроби.
, а также при нахождении производной произведения нескольких функций или производной дроби.
Пример.Найти производную функции 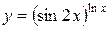 .
.
Решение.Функция 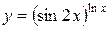 – степенно-показательная.
– степенно-показательная.
Прежде чем дифференцировать, прологарифмируем данную функцию:
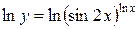 ;
;
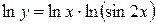 .
.
Дифференцируем как неявно заданную функцию:
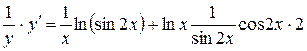
Из полученного равенства выразим 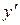 :
:
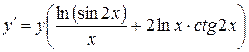
Вместо 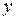 подставим
подставим 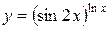 :
:
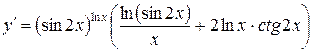 .
.
Пример.Найти производную функции 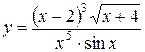 .
.
Решение.Прологарифмируем данную функцию
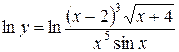 ;
;
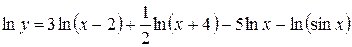 .
.
Дифференцируем:
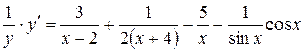
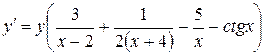
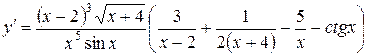 .
.
Дата добавления: 2021-09-25; просмотров: 554;











