Точки разрыва и их классификация

1. Если левосторонний предел функции 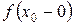и ее правосторонний предел 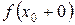существуют, но не равны между собой т.е.

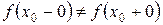
то точка называется точкой разрыва первого рода.

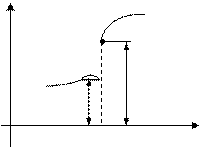
Геометрическая иллюстрация точки разрыва первого рода ясна из рисунка.

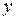
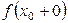
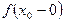
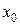
Пример. Какого рода разрыв в точке ?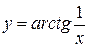

Решение. В точке 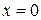функция 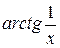не существует. Найдем левосторонний и правосторонний пределы функции

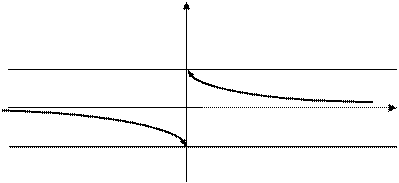
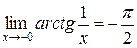, так как при 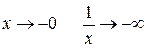, а ;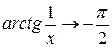

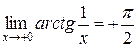, так как при 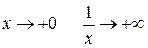, а .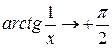

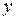
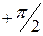
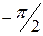
Таким образом, оба предела в точке 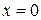существуют, но между собой не равны 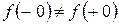, и точка 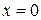является точкой разрыва первого рода.

2. Если в точке 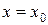существует левосторонний бесконечный или правосторонний бесконечный предел функции или оба левосторонний и правосторонний пределы являются бесконечными, то эта точка называется точкой разрыва второго рода.

Графики функций с точкой разрыва второго рода имеют вид:

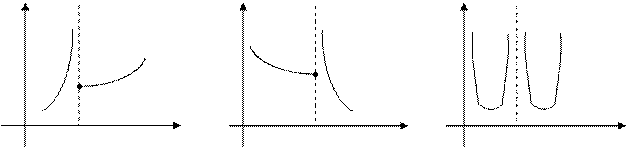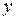
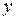
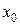
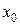
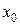
полагают 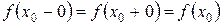, т.е. принимают, что .

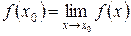КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какая классификация точек разрыва?

2. Сформулируйте определение непрерывности функции.

3. Какие пределы называются односторонними?

4. Какие пределы называются бесконечными?

ЛЕКЦИЯ 4. ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ СВОЙСТВА. ТАБЛИЦА ПРОИЗВОДНЫХ.

План