Асимптоты графика функции
5.5. Исследование функции и построение графика
5.1.Промежутки монотонности функции
Функция называется возрастающей (убывающей) в некотором промежутке, если в этом промежутке каждому большому значению аргумента соответствует большее (меньшее) значение функции.
Интервалы, на которых функция возрастает (убывает), называются интервалами монотонности функции.
Монотонность функции 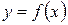 характеризуется знаком ее первой производной
характеризуется знаком ее первой производной 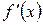 :
:
§ если в некотором промежутке 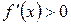 , то функция возрастает;
, то функция возрастает;
§ если в некотором промежутке 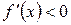 , то функция убывает.
, то функция убывает.
Таким образом, для промежутков монотонности функции  , надо:
, надо:
1) найти нули и точки разрыва производной функции 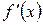 ;
;
2) определить знак 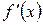 на каждом промежутке.
на каждом промежутке.
Пример.Найти промежутки монотонности функции 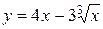 .
.
Решение.Дифференцируя данную функцию, находим
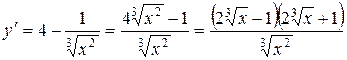 .
.
Найдем нули и точки разрыва функции:
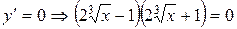 .
.
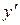 – не существует
– не существует 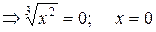 .
.
 Эти точки делят числовую ось на 4 промежутка:
Эти точки делят числовую ось на 4 промежутка: 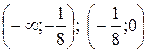 ;
;
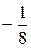 0
0 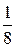

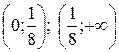 .
.
Методом проб определим знак 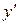 на каждом промежутке:
на каждом промежутке:
§ на 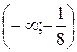 имеем
имеем 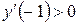 ; на
; на 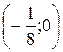 имеем
имеем 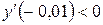 ;
;
§ на 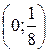 имеем
имеем 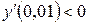 ; на
; на 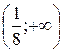 имеем
имеем 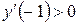 .
.
Таким образом, в промежутках 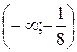 и
и 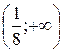 функция возрастает, в промежутках
функция возрастает, в промежутках 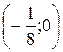 и
и 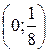 – убывает.
– убывает.
5.2. Экстремум функции
Пусть функция  непрерывна на некотором интервале
непрерывна на некотором интервале 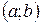 , содержащем точку
, содержащем точку  .
.
Точка 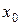 называется точкой максимума функции
называется точкой максимума функции  , если существует такая окрестность точки
, если существует такая окрестность точки  , что для всех точек
, что для всех точек 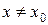 этой окрестности выполняется неравенство:
этой окрестности выполняется неравенство:
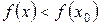 .
.
Точка 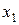 называется точкой минимума функции
называется точкой минимума функции  , если существует такая окрестность точки
, если существует такая окрестность точки 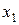 , что для всех
, что для всех 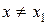 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство
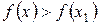 .
.
Точки минимума и максимума функции называют точками экстремума.
Функция  на данном промежутке может иметь несколько экстремумов, причем некоторые из минимумов функции могут быть больше некоторых из ее максимумов.
на данном промежутке может иметь несколько экстремумов, причем некоторые из минимумов функции могут быть больше некоторых из ее максимумов.
Точками экстремума могут служить только точки, принадлежащие области определения функции, в которых первая производная 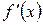 обращается в нуль или терпит разрыв. Такие точки называются критическими точками I-го рода.
обращается в нуль или терпит разрыв. Такие точки называются критическими точками I-го рода.
Точками экстремума являются лишь те из критических точек, при переходе через которые первая производная 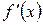 меняет знак, а именно, если при переходе через критическую точку
меняет знак, а именно, если при переходе через критическую точку 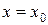 в положительном направлении знак
в положительном направлении знак 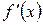 меняется с плюса на минус, то точка
меняется с плюса на минус, то точка 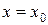 – точка максимума, если с минуса на плюс – минимума.
– точка максимума, если с минуса на плюс – минимума.
Правило нахождения экстремума функции:
1. Находим первую производную.
2. Находим нули и точки разрыва 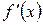 .
.
3. Определим знак производной в полученных промежутках.
4. Находим точки экстремума.
5. Находим значение функции в точках экстремума.
Пример.Найти экстремум функции 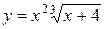 .
.
Решение. Функция определена на всей числовой оси.
1. Находим производную:
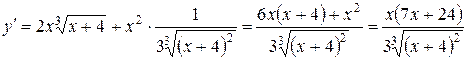 ;
;
2. Находим нули и точки разрыва производной:
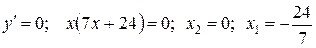 .
.
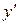 – не существует, если
– не существует, если 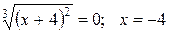 .
.
3. Точки разрыва и нули функции нанесем на числовую ось и определим знаки производной на промежутках

– 4 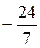 0
0 
4. Таким образом, точки 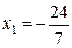 и
и 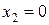 – являются точками экстремума, причем
– являются точками экстремума, причем 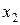 – точка минимума,
– точка минимума, 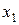 – максимума.
– максимума.
5. Найдем значение функции в точках экстремума:
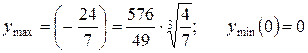 .
.
В точке 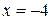 экстремума нет, т.к.
экстремума нет, т.к. 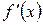 знака при переходе через точку
знака при переходе через точку 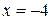 не меняет.
не меняет.
Следует отметить, что точки, в которых производная обращается в ноль, иногда проще исследовать на экстремум, выяснив знак второй производной 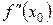 (второй достаточный признак): точка
(второй достаточный признак): точка 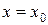 , в которой
, в которой 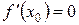 , а
, а 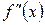 существует и отлично от нуля, является экстремальной, причем точкой максимума, если
существует и отлично от нуля, является экстремальной, причем точкой максимума, если 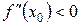 , и точкой минимума, если
, и точкой минимума, если 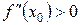 .
.
Пример. Найти экстремумы функции 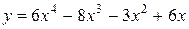 .
.
Решение. Область определения вся числовая ось. Найдем первую производную: 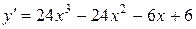 .
.
Найдем нули производной: 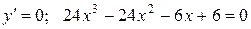 ;
;
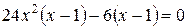 ;
;
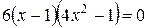 ;
;
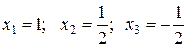 .
.
Найдем вторую производную: 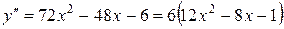 .
.
Найдем знак второй производной в критических точках
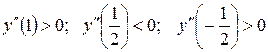 .
.
Таким образом, 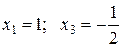 – точки минимума,
– точки минимума, 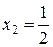 – точка максимума. Найдем экстремумы функции:
– точка максимума. Найдем экстремумы функции: 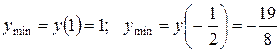 ;
;
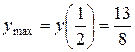 .
.
5.3.Выпуклость и вогнутость функции. Точки перегиба
Кривая называется выпуклой (вогнутой) в некотором промежутке, если она расположена ниже (выше) касательной, проведенной к кривой в любой точке этого промежутка. Выпуклость или вогнутость кривой  характеризуется знаком второй производной
характеризуется знаком второй производной 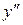 , а именно, если в некотором промежутке
, а именно, если в некотором промежутке 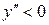 , то кривая выпукла, если
, то кривая выпукла, если 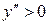 , то вогнута.
, то вогнута.
Точкой перегиба кривой называется такая ее точка, которая отделяет участок выпуклости от участка вогнутости.
Точками перегиба графика функции 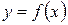 могут служить точки, находящиеся внутри области определения функции, в которых вторая производная
могут служить точки, находящиеся внутри области определения функции, в которых вторая производная 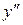 обращается в нуль или терпит разрыв, и при переходе через которые вторая производная
обращается в нуль или терпит разрыв, и при переходе через которые вторая производная 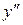 меняет знак.
меняет знак.
Таким образом, получаем правило отыскания промежутков выпуклости и вогнутости и точек перегиба графика функции.
1. Найти вторую производную функции 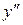 .
.
2. Найти точки, в которых вторая производная 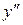 обращается в нуль или не существует.
обращается в нуль или не существует.
3. Определить знак второй производной на каждом промежутке.
4. Найти точки перегиба.
Пример. Исследовать на выпуклость, вогнутость и точки перегиба график функции 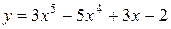 .
.
Решение.Область определения функции 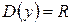 . Находим вторую производную, дифференцируя функцию дважды.
. Находим вторую производную, дифференцируя функцию дважды.
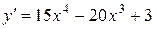
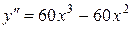
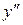 существует на всей оси и обращается в нуль в точках:
существует на всей оси и обращается в нуль в точках:
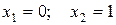 .
.
Определим знак второй производной на промежутках:

0 1 
На интервале 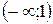 – функция выпукла, на интервале
– функция выпукла, на интервале 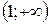 – вогнута. Точка с абсциссой
– вогнута. Точка с абсциссой 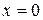 – не является точкой перегиба, т.к. вторая производная не меняет знак при переходе через нее.
– не является точкой перегиба, т.к. вторая производная не меняет знак при переходе через нее.
Точка с абсциссой 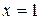 – точка перегиба. Найдем значение функции в этой точке.
– точка перегиба. Найдем значение функции в этой точке.
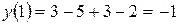 .
.
Таким образом, 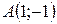 – точка перегиба.
– точка перегиба.
5.4.Асимптоты графика функции
Прямая называется асимптотой кривой 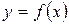 , если расстояние от точки
, если расстояние от точки 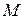 , лежащей на кривой, до этой прямой стремится к нулю при удалении точки
, лежащей на кривой, до этой прямой стремится к нулю при удалении точки 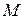 в бесконечность.
в бесконечность.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальной асимптотой является прямая 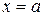 , проходящая через точку разрыва функции. Уравнение наклонной асимптоты имеет вид:
, проходящая через точку разрыва функции. Уравнение наклонной асимптоты имеет вид: 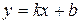 , де
, де 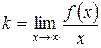 ;
; 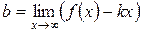 .
.
Прямая 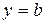 является горизонтальной асимптотой, если существует конечный предел функции при
является горизонтальной асимптотой, если существует конечный предел функции при 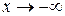 или
или 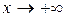 (горизонтальная асимптота – частный случай наклонной асимптоты при
(горизонтальная асимптота – частный случай наклонной асимптоты при 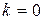 ).
).
Пример.Найти асимптоты кривой 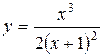 .
.
Решение.Кривая имеет вертикальную асимптоту 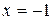 (в точке
(в точке 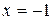 функция не существует). Найдем наклонные асимптоты
функция не существует). Найдем наклонные асимптоты 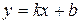 .
.
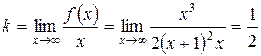 ;
;
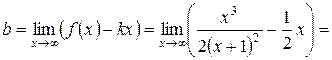
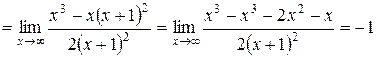 .
.
Таким образом, 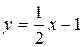 – наклонная асимптота
– наклонная асимптота
5.5. Исследование функции и построение графика
Общее исследование функции и построение ее графика выполняется по следующей схеме:
1. Найти область определения.
2. Проверить, не является ли функция четной или нечетной, периодической.
3. Найти промежутки монотонности функции и ее экстремумы.
4. Найти промежутки выпуклости и вогнутости графика функции и его точки перегиба.
5. Найти асимптоты графика функции.
6. Построить по полученным результатам график функции.
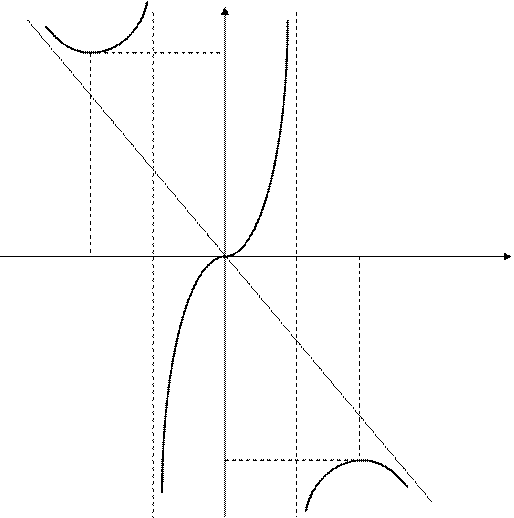
Пример.Исследовать функцию 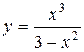 и построить график.
и построить график.
Решение.
1. Область определения 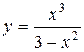 :
: 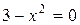 ;
; 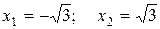 . Функция существует на интервалах:
. Функция существует на интервалах: 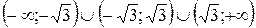 .
.
2. 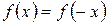 – условие четности;
– условие четности; 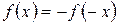 – условие нечетности
– условие нечетности
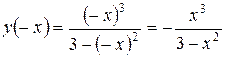 , т.е.
, т.е. 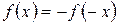 .
.
Функция нечетная, ее график симметричен относительно начала координат.
3. Находим первую производную
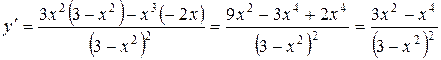 .
.
Найдем критические точки. Первую производную приравняем к нулю
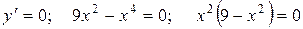
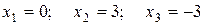 .
.
Таким образом, это критические точки. На числовую ось нанесем критические точки и точки разрыва.
Определим промежутки возрастания и убывания, точки экстремума (по знаку первой производной)

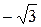 0
0 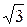 3
3 
Поскольку 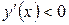 на интервалах
на интервалах 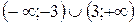 , то функция на них убывает, поскольку
, то функция на них убывает, поскольку 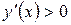 на интервале
на интервале 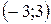 , то функция возрастает на этом интервале.
, то функция возрастает на этом интервале.
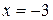 – точка минимума,
– точка минимума, 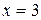 – точка максимума.
– точка максимума.
Найдем экстремум функции: 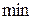 –
– 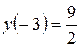 ;
; 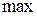 –
– 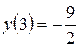 .
.
4. Находим вторую производную.
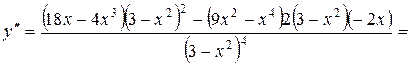
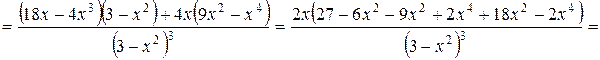
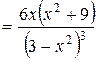 .
.
Найдем критические точки: 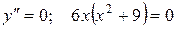 .
.
Таким образом, 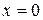 – критическая точка.
– критическая точка.
Определим знак 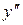 на промежутках
на промежутках

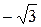 0
0 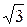

На интервалах 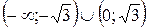 – график функции вогнутый. На интервалах
– график функции вогнутый. На интервалах 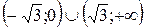 – выпуклый. Точка
– выпуклый. Точка 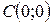 – точка перегиба.
– точка перегиба.
5. 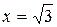 и
и 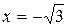 – вертикальные асимптоты (прямые, проходящие через точки разрыва).
– вертикальные асимптоты (прямые, проходящие через точки разрыва).
Найдем наклонные: 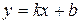 .
.
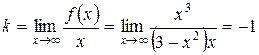
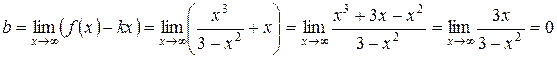
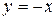 – наклонная асимптота.
– наклонная асимптота.
6. Строим график функции (рис.)
| 
| ||||||||||||||||||||||||||
| 4,5 | |||||||||||||||||||||||||||
– 3 
| 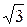
| 
| |||||||||||||||||||||||||
| -4,5 | |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Рисунок – График искомой функции
КОНТРОЛЬНЫЕ ВОПРОСЫ:
1. Какие существуют асимптоты графика функции?
2. Как найти выпуклость и вогнутость функции, точки перегиба?
3. Как найти экстремум функции?
Дата добавления: 2021-09-25; просмотров: 992;











