Переходные процессы в цепи с одним реактивным элементом
Здесь приведены примеры задач с индуктивным элементом, аналогичные задачи могут быть рассмотрены и для цепей с емкостным элементом.
1. Короткое замыкание цепи
Рассмотрим следующую цепь.
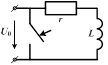
| При коротком замыкании цепи с последовательным соединением r и L уравнение переходного тока i, равного в этом случае свободному току i", имеет вид:
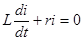
|
Характеристическое уравнение 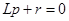 имеет корень
имеет корень 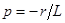 , тогда
, тогда
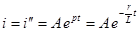
Если до момента короткого замыкания по цепи шел постоянный ток 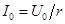 , где
, где 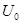 – постоянное напряжение цепи, это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования:
– постоянное напряжение цепи, это значение тока сохранится и для первого мгновения после замыкания цепи, откуда определяется постоянная интегрирования: 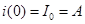 .
.
| Следовательно, 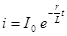 , ,
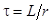 называется постоянной времени.
В цепи появляется э. д. с. самоиндукции: называется постоянной времени.
В цепи появляется э. д. с. самоиндукции:
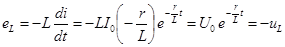 . .
|
Энергия, расходуемая на нагрев сопротивления r цепи за время переходного процесса равна энергии, запасенной в индуктивности до замыкания цепи:
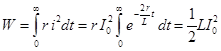
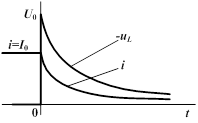
2. Включение цепи на постоянное напряжение
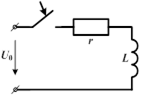
| При включении цепи r, L на постоянное напряжение 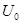 вынужденный ток вынужденный ток 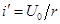 , а переходный ток , а переходный ток
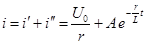 . .
|
Ток до переходного процесса, а следовательно, и в первый момент после включения равен нулю:
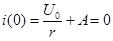 ,
,
откуда 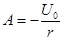 и
и 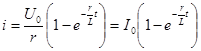 ,
,
т. е. переходный ток постепенно нарастает до своего окончательного значения 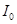 и тем медленней, чем больше постоянная времени t.
и тем медленней, чем больше постоянная времени t.
Напряжения на участках цепи
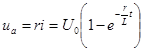 ;
; 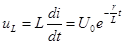
Следовательно, в первый момент напряжение цепи целиком сосредоточивается на индуктивности и затем постепенно переходит на сопротивление.
3. Включение цепи на синусоидальное напряжение
Пусть цепь r, L включается на синусоидальное напряжение 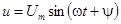 . Тогда значение напряжения в момент включения
. Тогда значение напряжения в момент включения 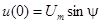 определяется величиной начальной фазы y, которая в этом случае называется также фазой включения.
определяется величиной начальной фазы y, которая в этом случае называется также фазой включения.
Вынужденный ток (в случае активно-индуктивного характера цепи ток отстает от напряжения):
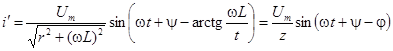
Переходный ток: 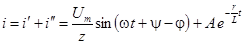 .
.
Учет начального условия дает: 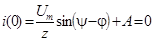 Þ
Þ 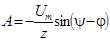
и окончательно 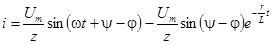 .
.
Переходное напряжение на активном сопротивлении пропорционально току, а на индуктивности есть
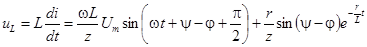 .
.
При включении в момент времени, когда вынужденный ток равен нулю, например при 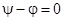 , уравнения принимают вид
, уравнения принимают вид
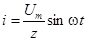 и
и 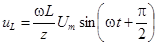 ,
,
т. е. свободного тока и свободных напряжений на участках цепи нет, и сразу после включения наступает установившийся процесс.
В общем же случае на синусоидальные установившиеся напряжения на участках цепи и ток налагаются свободные составляющие, значения которых уменьшаются по показательному закону. В результате ток i и напряжения 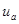 и
и 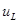 в течение некоторых промежутков времени могут превосходить их максимальные значения
в течение некоторых промежутков времени могут превосходить их максимальные значения 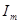 ,
, 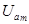 и
и 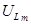 при установившемся режиме. В результате может возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения y и от постоянной времени t, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
при установившемся режиме. В результате может возникнуть большой ток, называемый сверхтоком, и перенапряжения. Их величина зависит от фазы включения y и от постоянной времени t, определяющих, соответственно, начальные значения свободных составляющих и скорость их уменьшения.
Так, при включении в момент времени, когда вынужденный ток получает максимальное значение 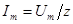 , например при
, например при 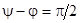 ,
,
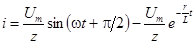 ;
; 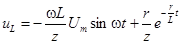
При большой постоянной времени получается большой сверхток, однако он не может превзойти двойную амплитуду 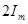 установившегося тока.
установившегося тока.
Дата добавления: 2019-12-09; просмотров: 411;











