Переходные процессы в линейных электрических цепях с двумя реактивными элементами
Рассмотрим характер этих процессов на примере короткого замыкания цепи с последовательным соединением индуктивности и емкости.
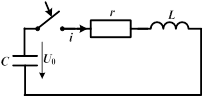
| Пусть емкость, заряженная до напряжения 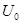 , замыкается на цепь с последовательным соединением сопротивления и индуктивности. Тогда уравнение по второму закону Кирхгофа будет однородным: , замыкается на цепь с последовательным соединением сопротивления и индуктивности. Тогда уравнение по второму закону Кирхгофа будет однородным: 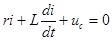 , откуда , откуда 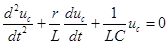 . .
|
Характеристическое уравнение 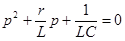 имеет два корня:
имеет два корня:
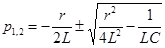 .
.
Если 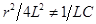 т.е.
т.е. 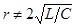 , корни будут различными
, корни будут различными 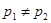 .
.
В этом случае решение дифференциального уравнения 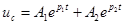 , а ток в цепи
, а ток в цепи 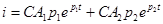
В момент t = 0 напряжение на емкости и ток индуктивности, равный току всей цепи, будут такими же, как и до замыкания:
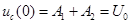 ,
, 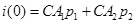
откуда постоянные интегрирования 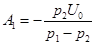 ,
, 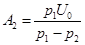
и, следовательно, ток и напряжения на участках будут:
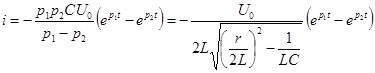 ;
; 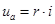 ;
;
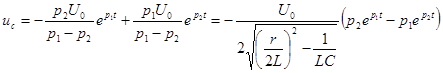 ;
;
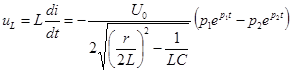
Характер переходного процесса зависит от соотношения между параметрами r, L и С.
1. Если 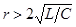 , корни
, корни 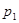 и
и 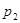 будут вещественными, причем
будут вещественными, причем 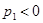 ,
, 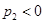 ,
, 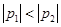 .
.
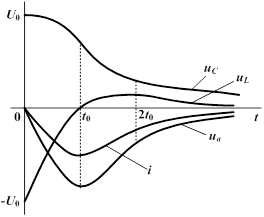
| Напряжение конденсатора, начиная с 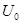 , непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение на сопротивлении, начинаясь с нуля, всегда отрицательны, что соответствует току разряда. Напряжение , непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положительная и больше второй отрицательной. Ток i цепи и напряжение на сопротивлении, начинаясь с нуля, всегда отрицательны, что соответствует току разряда. Напряжение 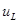 на индуктивности возникает скачком, принимая значение на индуктивности возникает скачком, принимая значение 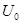 ; проходит через нуль в момент ; проходит через нуль в момент 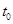 при равенстве значений своих экспонент, т.е. при при равенстве значений своих экспонент, т.е. при 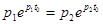 ,откуда ,откуда 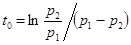 и затем становится положительным. и затем становится положительным.
|
Так как 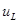 пропорционально производной от тока, то в момент времени
пропорционально производной от тока, то в момент времени 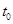 абсолютное значение тока проходит через максимум. Приравняв производную
абсолютное значение тока проходит через максимум. Приравняв производную 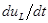 нулю, можно видеть, что
нулю, можно видеть, что 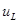 имеет максимум при
имеет максимум при 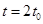 .
.
Рассмотренный вид разряда называется апериодическим.
2. Пусть 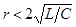 .
.
Введем обозначения: 
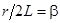 ,
, 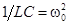 ,
, 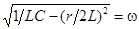 .
.
Тогда выражение для корней характеристического уравнения можно переписать следующим образом:
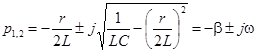
Так как w – число вещественное, корни 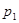 и
и 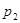 будут комплексными. После подстановки значений
будут комплексными. После подстановки значений 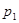 и
и 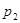 выражения для тока и напряжений на участках примут вид:
выражения для тока и напряжений на участках примут вид:
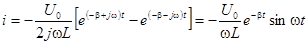 ,
, 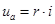 ,
,
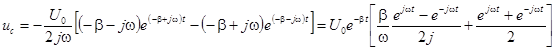 .
.
Обозначим 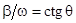
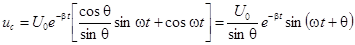 .
.
Аналогично
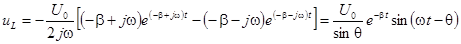 .
.
Ток и напряжения цепи, в которой 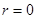 и, следовательно,
и, следовательно, 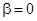 ,
, 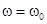 ,
, 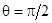 :
:
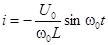 ,
, 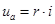 ,
,  ,
, 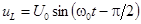 .
.
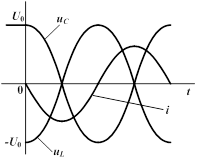
Следовательно, если бы в цепи не происходило рассеяние энергии, ток и напряжения на участках были бы синусоидальными функциями времени, т.е. имели бы место собственные незатухающие колебания, угловая частота которых равна резонансной частоте этой цепи 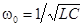 . Для незатухающих колебаний векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости аналогичны тем, которые имеют место при резонансе в цепи с последовательным соединением r, L и С. Следовательно, и здесь происходит полный обмен энергиями между С и L. . Для незатухающих колебаний векторная диаграмма и график мгновенных значений тока и напряжений на индуктивности и емкости аналогичны тем, которые имеют место при резонансе в цепи с последовательным соединением r, L и С. Следовательно, и здесь происходит полный обмен энергиями между С и L.
| 
|
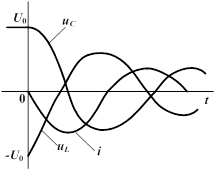
| Если в цепи есть сопротивление 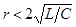 , разряд также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как , разряд также носит колебательный характер, но амплитуды тока и напряжений постепенно уменьшаются, так как 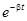 с ростом t стремится к нулю. Угловая частота этих собственных затухающих колебаний с ростом t стремится к нулю. Угловая частота этих собственных затухающих колебаний 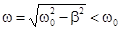 . Энергетический процесс заключается в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда запасенная энергия полностью рассеется. . Энергетический процесс заключается в обмене энергиями между емкостью и индуктивностью с непрерывным рассеянием энергии сопротивлением. Переходный процесс закончится, когда запасенная энергия полностью рассеется.
|
3. Если 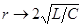 , частота
, частота 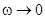 и в выражении для тока возникает неопределенность:
и в выражении для тока возникает неопределенность: 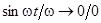 . Такой режим разряда называется критическим.
. Такой режим разряда называется критическим.
Раскрывая неопределенность 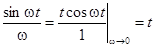 , для этого случая получаем:
, для этого случая получаем:
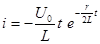 ,
, 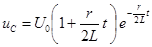 ,
, 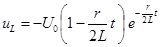 .
.
Характер разряда будет апериодическим.
Дата добавления: 2019-12-09; просмотров: 456;











