Последовательность расчета операторным методом

Расчет переходных процессов в сложных цепях операторным методом состоит из двух основных этапов:

1) составления изображения искомой функции времени.

Для этого записываются законы Кирхгофа и соответствующая им алгебраическая система уравнений для изобра­жений. При этом необходимо учесть ненулевые начальные условия. Решение си­стемы дает изображения искомых токов и напряжений. Эти изображения имеют вид рацио­нальных дробей.

2) переход от изображения к функции времени.

Для перехода от изображений к оригиналам можно использовать таблицы, приведенные в справочниках или, в случае сложного вида функции воспользоваться теоремой разложения.

Теорема разложения

В большинстве случаев изображение представляет собой правильную дробь:

,

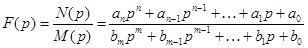у которой .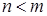

Если полином 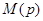не имеет кратных корней, то такая дробь может быть разложена на простые дроби:

,

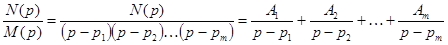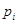- корни уравнения 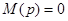, коэффициенты A_k: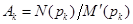

Тогда для оригиналов можно записать следующее выражение:

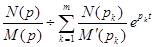
Это и есть теорема разложения, позволяющая по изоб­ражению в виде рациональной дроби найти оригинал. Если при этом один из корней 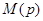равен нулю, соответ­ствующая показательная функция превращается в постоянную вели­чину.