Мощность периодических несинусоидальных напряжений и токов

Активная мощность периодических функций напряжения и тока произвольной формы определяется как средняя мощность за период:

.

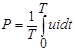Если напряжение и ток состоят из ряда гармонических составляющих, то под знаком интеграла окажется сумма произведений гармонических равных частот:

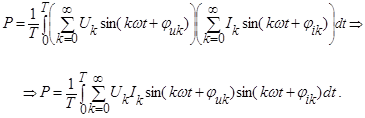
После интегрирования приходим к следующему результату:

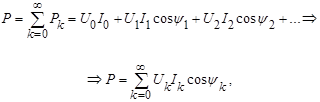
где .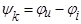

Здесь постоянные составляющие 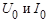рассматриваются как гармонические составляющие с нулевой частотой.

Аналогично реактивная мощность определится как сумма реактивных мощностей отдельных гармоник:

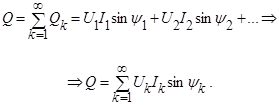
Полная мощность определится как произведение действующих значений напряжения и тока:

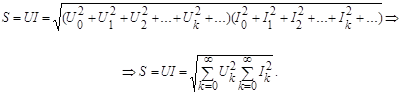
Для несинусоидальных функций в отличие от синусоидальных квадрат полной мощности обычно больше суммы квадратов активной и реактивной мощностей 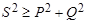, поэтому вводят еще один вид мощности, которую называют мощностью искажения, определяемую из соотношения:

.

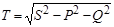АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ КЛАССИЧЕСКИМ МЕТОДОМ

Общие сведения

Под переходным процессом понимают процесс перехода от одного режима работы электрической цепи (обычно периодического) к другому (обычно также периодическому), чем-либо отличающемуся от предыдущего, например, амплитудой, фазой, формой или частотой действующей в схеме э.д.с., значениями параметров схемы, а также вследствие конфигурации цепи.

Физически переходные процессы представляют собой переход от одного энергетического состояния, соответствующего докоммутационному режиму, к другому энергетическому состоянию, соответствующему послекоммутационному режиму.

Энергия магнитного поля, создаваемого током i, протекающим через индуктивность L: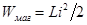

Энергия электрического поля, возникающего вследствие того, что к конденсатору емкостью C приложено напряжение : .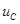

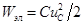Энергии электрического и магнитного полей не могут меняться скачком на конечную величину за бесконечно малый промежуток времени, поэтому не могут меняться скачком ток в цепи с индуктивностью и напряжение на конденсаторе.

Тем самым, мы получаем два закона коммутации:

1. Ток через индуктивный элемент L непосредственно до коммутации равен току через этот же индуктивный элемент после коммутации, что принято записывать следующими образом: 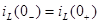(момент времени непосредственно до коммутации и непосредственно после).

2. Напряжение на конденсаторе непосредственно до коммутации равно напряжению на этом конденсаторе после коммутации: .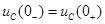

Для расчета переходных процессов в цепях составляется система уравнений по законам Ома и Кирхгофа для мгновенных значений напряжений и токов. Эта система приводится к одному уравнению для одного из напряжений или токов. Поскольку мы будем пока рассматривать линейные цепи, то итоговое уравнение будет линейным дифференциальным уравнением. Порядок этого уравнения равен числу независи­мых начальных условий для токов индуктивностей и напряжений на емкостях.

Решение линейных дифференциаль­ных уравнений с постоянными коэффициентами представляет собой сумму частного решения неоднородного уравнения 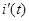и общего решения однородного уравнения 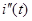. Т.о,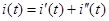

Частное решение неоднородного уравнения определяется видом функции, стоящей в правой части уравнения, и поэтому называется вынужденным. Для цепей с заданными постоянными или периодическими напряжениями (токами) источников энергии выну­жденное решение совпадает с установившимися значениями искомых величин. Оно может быть найдено теми способами расчета, которые вы рассматривали в прошлом семестре.

Общее решение i" однородного уравнения описывает процесс, про­исходящий без воздействия внешних источников за счет изменения запаса энергии, накопленной в цепи до начала переходного про­цесса; оно имеет одинаковый вид для любого переходного процесса в данной цепи. Это решение называют свободной состав­ляющей переходного процесса.

Решение однородного дифференциального уравнения ищется в виде

,

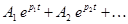где 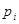– корни характеристического уравнения.

По­стоянные интегрирования 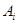, входящие в выражение для переходной величины, определяют из начальных условий – значе­ний напряжений на емкостях и токов в индуктивностях, которые в соответствии с законами коммутации не могут изменяться скачком.