Разложение периодических функций в ряд Фурье
Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону. Явления, происходящие в линейных цепях при периодических, несинусоидальных напряжениях и токах проще всего поддаются исследованию, если кривые напряжения или тока разложить в тригонометрический ряд Эйлера - Фурье.
Как известно из курса математики, всякую периодическую функцию 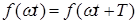 с периодом
с периодом 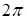 , удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Этот ряд состоит из суммы постоянной составляющей А0 (нулевая гармоника) и синусоид разных частот (гармоник)
, удовлетворяющую условиям Дирихле, можно разложить в ряд Фурье. Этот ряд состоит из суммы постоянной составляющей А0 (нулевая гармоника) и синусоид разных частот (гармоник) 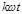 .
.
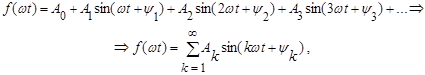 (*)
(*)
где k – целые числа, начиная с единицы, 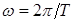 - основная частота, Т - период функции.
- основная частота, Т - период функции.
Здесь составляющая 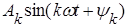 при k = 1 носит название первой гармоники, все остальные члены вида
при k = 1 носит название первой гармоники, все остальные члены вида 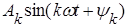 при k > 1 носят название высших гармоник. Гармоники для которых k - нечетное число, называются нечетными, а для которых k - четное число, называются четными.
при k > 1 носят название высших гармоник. Гармоники для которых k - нечетное число, называются нечетными, а для которых k - четное число, называются четными.
Суммы синусов с вспомогательными углами 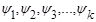 можно представить рядом Фурье, имеющим следующую форму:
можно представить рядом Фурье, имеющим следующую форму:
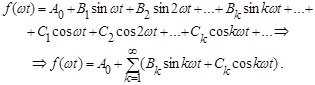 (**)
(**)
Здесь 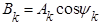 ;
; 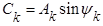 .
.
Коэффициенты 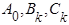 могут быть вычислены при помощи следующих интегралов:
могут быть вычислены при помощи следующих интегралов:
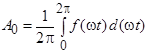 ;
; 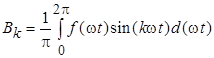 ;
; 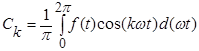 .
.
Постоянная составляющая 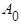 равна среднему значению функции
равна среднему значению функции 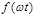 за ее период
за ее период 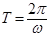 .
.
Зная коэффициенты ряда (**) можно перейти к форме (*), вычисляя
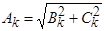 и
и 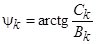 .
.
В том случае, если периодическая функция задана не аналитически, а в виде графической кривой, то при разложении ее в ряд Фурье коэффициенты ряда можно отыскать приближенно, заменяя интегралы суммой. В этом случае период Т кривой на графике разбивают на n равных частей, после чего коэффициенты 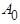 ,
, 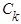 ,
, 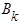 находят из выражений, где вместо
находят из выражений, где вместо 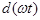 следует подставить
следует подставить 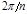 .
.
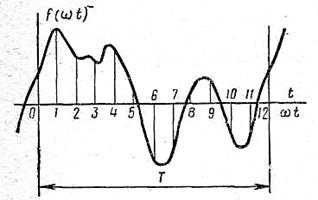
| 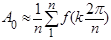 ; ;
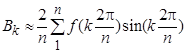 ; ; 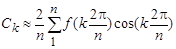 . .
|
Дата добавления: 2019-12-09; просмотров: 441;











