Законы электрических цепей в операторной форме

Пусть цепь с последовательным соединением r, L, С при ненулевых начальных условиях включается на напряжение 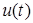. Тогда

Применим к этому уравнению изображение Лапласа. Преобразование Лапласа является линейным, поэтому изображение суммы равно сумме изображений:

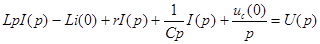
В результате вместо интегро-дифференциального уравнения получаем алгебраическое, откуда ток в такой цепи есть:

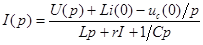
Это выражение представляет собой аналог закона Ома в оператор­ной форме для переходного процесса при ненулевых начальных условиях. В знаменателе стоит операторное сопротивле­ние: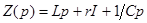

В общем случае сложной цепи ее операторное сопротивление имеет вид:

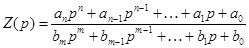
Первый закон Кирхгофа в операторном виде: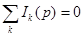

Второй закон Кирхгофа в операторном виде при нулевых начальных условиях и отсутствии взаимной ин­дукции имеет вид:

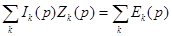
При составлении операторных уравнений удобнее использовать операторные схемы замещения, которые составляются на основе заданной электрической схемы для оригиналов. Сопротивления элементов ветвей записываются в операторной форме: R, pL, 1/pC. Изображения заданных ЭДС и токов находят, как правило, по таблицам. Ненулевые начальные условия учитывают введением дополнительных источников ЭДС (внутренних ЭДС). Полученную операторную схему рассчитывают по законам Кирхгофа в операторной форме или любым другим методом, используемым при расчете цепей постоянного тока.