Холостой ход и короткое замыкание четырехполюсника
При холостом ходе ток на выходе 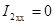 и уравнения четырехполюсника дают
и уравнения четырехполюсника дают 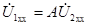 ,
, 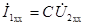 .
.
При коротком замыкании напряжение на выходе 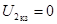 и из уравнений четырехполюсника вытекает, что
и из уравнений четырехполюсника вытекает, что 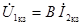 ,
, 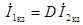 .
.
Отсюда видно, что параметр A представляет собой отношение входного и выходного комплексных напряжений при холостом ходе четырехполюсника, a D – отношение входного и выходного комплексных токов при коротком замыкании.
Если при холостом ходе напряжение на выходе будет равно напряжению 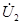 при нагрузке, а при коротком замыкании ток на выходе – току
при нагрузке, а при коротком замыкании ток на выходе – току 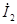 при нагрузке, уравнения четырехполюсника получают вид:
при нагрузке, уравнения четырехполюсника получают вид:
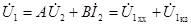 ,
, 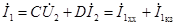
Следовательно, напряжение 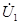 и ток
и ток 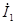 при любом заданном режиме работы приемника (
при любом заданном режиме работы приемника ( 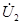 и
и 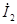 ) могут быть определены путем наложения соответствующих режимов холостого хода и короткого замыкания.
) могут быть определены путем наложения соответствующих режимов холостого хода и короткого замыкания.
Чтобы осуществить это наложение, надо знать, как расположить друг относительно друга векторные диаграммы холостого хода и короткого замыкания Для этой цели нужно измерить сдвиг фаз σ между векторами 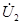 и
и 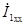 при опыте холостого хода и сдвиг фаз β между векторами
при опыте холостого хода и сдвиг фаз β между векторами 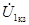 и
и 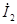 при опыте короткого замыкания.
при опыте короткого замыкания.
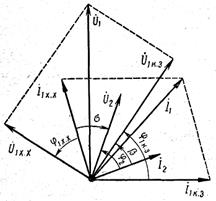
| После этого построение ведется в следующем порядке: строится заданная диаграмма 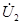 и и 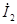 , затем под углом σ к вектору , затем под углом σ к вектору 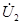 строится вектор строится вектор 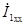 , а под углом , а под углом 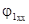 к нему вектор к нему вектор 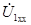 .Далее под углом β к вектору .Далее под углом β к вектору 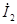 строится вектор строится вектор 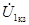 ,а под углом ,а под углом 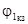 к нему – вектор к нему – вектор 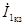 . После этого строятся векторы напряжения и тока на входе ( . После этого строятся векторы напряжения и тока на входе ( 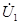 и и 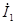 ) как суммы напряжений и токов при холостом ходе и коротком замыкании. ) как суммы напряжений и токов при холостом ходе и коротком замыкании.
|
Так как в симметричном четырехполюснике А = D, то
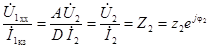
т. е. угол сдвига фаз между векторами 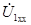 и
и 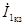 равен заданному углу φ2 сдвига фаз в нагрузке, что сразу определяет взаимное расположение векторных диаграмм холостого хода и короткого замыкания без добавочных измерений.
равен заданному углу φ2 сдвига фаз в нагрузке, что сразу определяет взаимное расположение векторных диаграмм холостого хода и короткого замыкания без добавочных измерений.
Указанное применение принципа наложения имеет большое значение при испытании мощных электротехнических устройств, описываемых линейными уравнениями, так как позволяет заменить опыт нагрузки, требующий источников большой мощности, опытами холостого хода и короткого замыкания при значительно меньшей мощности.
Дата добавления: 2019-12-09; просмотров: 549;











