Уравнения четырехполюсников
Электрическая цепь, имеющая два входных и два выходных зажима, называется четырехполюсником.
Активные четырехполюсники содержат внутри себя также источники электрической энергии. Соответственно, пассивные четырехполюсники внутри себя источников энергии не содержат. Примером их могут служить линия передачи, трансформатор, мостовая схема.
Принято изображать 4-полюсник в виде прямоугольника с двумя парами зажимов.
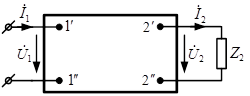
| 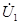 и и 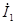 – комплексные напряжение и ток на входе четырехполюсника, – комплексные напряжение и ток на входе четырехполюсника, 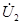 и и 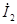 – комплексные напряжение и ток на его выходе, – комплексные напряжение и ток на его выходе, 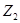 – комплексное сопротивление нагрузки. – комплексное сопротивление нагрузки.
|
Для вывода уравнений, связывающих входные и выходные напряжения и токи, удобно заменить приемник 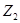 с напряжением
с напряжением 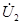 эквивалентным источником напряжения без внутреннего сопротивления с ЭДС равной
эквивалентным источником напряжения без внутреннего сопротивления с ЭДС равной 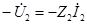 .
.
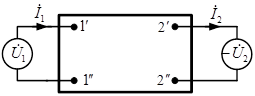
| Применим метод наложения. Сначала учитываем только источник 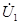 . Замыкая накоротко зажимы источника . Замыкая накоротко зажимы источника 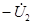 , находим токи , находим токи 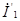 и и 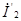 , которые, будут пропорциональны напряжению , которые, будут пропорциональны напряжению 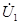 : :
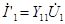 , , 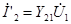
|
Аналогично, при наличии источника 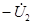 и коротком замыкании
и коротком замыкании 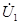 :
:
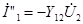 ,
, 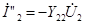
Здесь 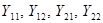 –комплексные коэффициенты пропорциональности, имеющие размерность проводимости;
–комплексные коэффициенты пропорциональности, имеющие размерность проводимости; 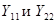 называются входными, a
называются входными, a 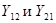 взаимными проводимостями. Проводимости
взаимными проводимостями. Проводимости 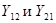 определяют токи в короткозамкнутом выходном или входном контуре при заданном напряжении в другом контуре.
определяют токи в короткозамкнутом выходном или входном контуре при заданном напряжении в другом контуре.
При одинаковом напряжении U токи 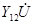 и
и 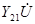 по принципу взаимности были бы равны между собой. Следовательно, взаимные проводимости:
по принципу взаимности были бы равны между собой. Следовательно, взаимные проводимости: 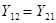 .
.
Действительные токи на входе и выходе четырехполюсника
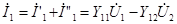 и
и 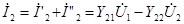 .
.
Совместное решение этих уравнений дает
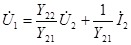 ,
,
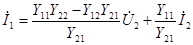 .
.
После введения обозначений
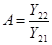 ,
, 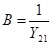 ,
, 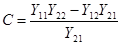 и
и 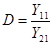
получаются уравнения четырехполюсника:
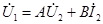 ,
, 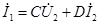
где комплексы А, В, С, D называются параметрами четырехполюсника. Между ними существует следующая связь:
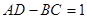 .
.
Следовательно, из четырех параметров независимыми являются три.
В симметричном четырехполюснике, который со стороны выходных зажимов представляет ту же цепь, что и со стороны входных,
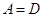 и
и 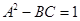 .
.
С помощью уравнений четырехполюсника можно определить нагрузочный режим, т. е. найти 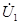 и
и 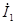 для заданных
для заданных 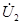 и
и 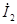 или две любые величины из указанных, если заданы две другие.
или две любые величины из указанных, если заданы две другие.
Дата добавления: 2019-12-09; просмотров: 429;











