Интерференция волн.

Когерентностьюназывается согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов, проявляющееся при их сложении.

Пусть в данную точку пространства приходят две световые волны Е₁ и Е₂ одинаковой частоты, которые возбуждают в этой точке колебания одинакового направления (обе волны поляризованы одинаковым образом):

Е₁ = А₁соs(wt + a₁),

Е₂ = A₂cos(wt + a₂).

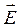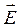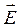Согласно принципу суперпозиции, напряженность результирующего поля равна = ₁ + ₂. Тогда амплитуда А результирующего колебания той же частоты может быть определена из выражения:

А² = А₁² +А₂² + 2А₁А₂соsj, (7.1)

где j = a₁ - a₂ = const.

Если частоты колебаний в обеих волнах w одинаковы, а разность фаз j возбуждаемых колебаний остается постоянной во времени, то такие волны называются когерентными.Дляэлектромагнитных волн существует дополнительное ограничение – не дают интерференционной картины когерентные волны ортогональной поляризации.

Приналожении когерентных волн они дают устойчивое колебание с неизменной амплитудойА = соnst, определяемой выражением (7.1) и в зависимости от разности фаз колебаний лежащей в пределах

|а₁ –А₂ê £ A £ а₁ +А_2.

Таким образом, когерентные волны при интерференции друг с другом дают устойчивое колебание с амплитудой не больше суммы амплитуд интерферирующих волн.

Если j = p, тогда соsj = -1, и А₁ = А₂, то амплитуда суммарного колебания равна нулю, и интерферирующие волны полностью гасят друг друга.

В случае некогерентных волн j непрерывно изменяется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение <cоsj>_t = 0. Поэтому слагаемое 2А₁А₂соsj в уравнении (7.1) равно нулю и

<А²> = <А₁²> + <А₂²>,

откуда интенсивность, наблюдаемая при наложении некогерентных волн, равна сумме интенсивностей, создаваемых каждой из волн в отдельности:

I = I₁ + I₂ .

В случае когерентных волн, соsj имеет постоянное во времени значение (но свое для каждой точки пространства), так что

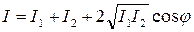. (7.2)

В тех точках пространства, для которых соsj > 0, I > I₁ +I₂; в точках, для которых соsj < 0, I < I₁+I₂. При наложении когерентных световых волн происходит перераспределение энергии светового потока в пространстве (при глобальном выполнении закона сохранения энергии), в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности (наблюдается интерференционная картина).Это явление называется интерференцией волн. Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: I₁ = I₂. Тогда согласно (7.2) в максимумах I = 4I₁, в минимумах же I = 0. Для некогерентных волн при том же условии получается всюду одинаковая интенсивность I = 2I₁.

Если имеются отклонения от сформулированных условий когерентности, например, частоты двух складываемых монохроматических волн несколько отличаются, то интерференционная картина может становиться неустойчивой, возникает эффект плывущей картины. Если же частоты складываемых волн совпадают, но разность фаз между ними изменяется со временем, то интерференционная картина, как правило, остается стационарной, но ее контрастность (соотношение интенсивностей соседних максимумов и минимумов) уменьшается.

Все естественные источники света (Солнце, лампочки накаливания и т.д.) не излучают электромагнитных волн одной определенной и строго постоянной частоты, поэтому световые волны, излучаемые любыми независимыми естественными источниками света, всегда некогерентны и, используя два таких источника, невозможно получить интерференцию света.

Некогерентность естественных источников света обусловлена тем, что излучение светящегося тела слагается из волн, испускаемых многими атомами. Отдельные атомы излучают цуги волн длительностью порядка 10^-8 с и протяженностью около 3 м. Фаза нового цуга никак не связана с фазой предыдущего цуга. В испускаемой телом световой волне излучение одной группы атомов через время порядка 10^-8 с сменяется излучением другой группы, причем фаза результирующей волны претерпевает случайные изменения. Когерентность существует только в пределах одного цуга. Средняя продолжительность одного цуга τ называется временем когерентности. Если волна распространяется в однородной среде, то фаза колебаний в какой-либо определенной точке пространства остается постоянной только в течение времени когерентности. За это время волна распространяется на расстояние l_ког = Vτ, называемое длиной когерентности (или длиной цуга). Колебания в точках, удаленных друг от друга на расстояниях, больших длины когерентности вдоль направления распространения волны, будут некогерентными.

Лазерное излучение характеризуется высокой степенью монохроматичности, т.е. излучение происходит на одной определенной и строго постоянной частоте, поэтому можно наблюдать интерференцию световых пучков, излучаемых двумя разными лазерами.

А как можно, пользуясь обычными некогерентными излучателями света, создать взаимно когерентные источники?

Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником света, на две части. Если заставить эти две волны пройти разные оптические пути, а потом наложить их друга на друга, то наблюдается интерференция волн. Разность оптических длин путей, проходимых интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн. Если эта разность ³ 1м, то будет наблюдаться наложение колебаний, соответствующих разным цугам, разность фаз между которыми будет непрерывно изменяться хаотическим образом, и интерференция волн не наблюдается.

Пусть разделение на две когерентные волны происходит в точке О (рис.7.2).

До точки Р первая волна проходит в среде споказателем преломления n₁ путь S₁, вторая волна проходит в среде с показателем преломления n₂ путь S₂. Если в точке О фаза колебания равна wt, то первая волна возбудит в точке Р колебание А₁соsw(t – S₁/V₁), а вторая волна – колебание А₂соsw(t – S₂/V₂), где V₁ и V₂ - фазовые скорости волны в первой и второй средах соответственно.

Рис.7.2.

Следовательно, разность фаз колебаний, возбуждаемых волнами в точке Р, будет равна:

j = w(S₂/V₂ – S₁/V₁) = (w/c)(n₂S₂ – n₁S₁).

Заменим w/с через 2pn/с = 2p/l_о, тогда

j = (2p/l_о)D, (7.3)

где D= n₂S₂ - n₁S₁ = L₂ - L₁ – величина, равная разности оптических длин проходимых волнами путей, и называется оптической разностью хода.

Из (7.3) видно, что если оптическая разность хода равна целому числу длин волн в вакууме:

D = ±ml_о (m = 0,1,2,…), (7.4)

то разность фаз оказывается кратной 2p и колебания, возбуждаемые в точке Р обеими волнами, будут происходить с одинаковой фазой. Таким образом, (7.4) есть условие интерференционного максимума.