Вопрос 3. Принцип суперпозиции волн. Групповая скорость. Стоячие волны.

Принцип суперпозиции.Если свойства среды не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения волн):при распространении в такой среде нескольких волн, каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды равно геометрической сумме смещений частиц.

Строго монохроматическаяволна имеет постоянную частоту. Будем рассматривать такие волны с учетом начальной фазы α:

ξ = А₀cos(ωt − kx + α). (1.5)

Значение фазовой скорости этой волны

V = ω/k или V = λν = λ/T.

С помощью такой волны нельзя передавать сигнал, так как в любой точке волны сигналы одинаковы. Сигнал должен отличаться, быть знаком (меткой) на волне. Но тогда волна уже не будет описываться уравнением (1.5).

Групповая скорость.Сигнал (импульс) можно представить (согласно теореме Фурье) в виде суперпозиции гармонических волн с частотами, заключенными в некотором интервале Δω. Суперпозиция волн, мало отличающихся друг от друга по частоте (т.е. ∆ω<<ω), называется волновым пакетом или группойволн (рис. 1.6). Выражение для группы волн имеет вид:

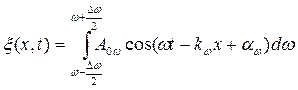. (1.6)

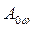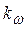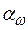Здесь , и – соответственно амплитуды, волновые числа и

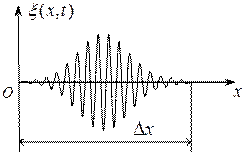Рис. 1.6

начальные фазы волн, составляющих группу.

Индекс 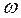при 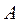, , 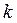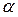указывает на то, что эти величины для разных частот различны.

Группе волн предписывают скорость u, с которой перемещается центр группы волн (волнового пакета), т.е. точка с максимальным значением 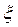. Эту скорость называют групповой скоростью. Этот волновой пакет может быть суммой нескольких волн (рис. 1.6) или, в частности, двух волн (рис. 1.7) с мало отличающимися частотами.

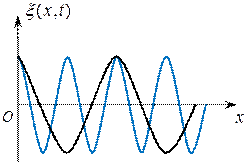Рис. 1.7

Среды, для которых групповая скорость зависит от частоты, называются диспергирующими средами, т.е. средами, обладающими дисперсией.

В недиспергирующей средевсе плоские волны, образующие пакет,

распространяются с одинаковой фазовой скоростью V. Очевидно, что в данном случае направление скорости перемещения пакета совпадает с направлением скорости 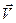. Следует отметить, что всякий волновой пакет в каждый момент времени занимает ограниченную область пространства.

В диспергирующей средекаждая волна распространяется со своей скоростью, пакет с течением времени расплывается, его ширина увеличивается. Если дисперсия невелика, то расплывание происходит не слишком быстро и пакету можно приписать скорость u. Вместе с движением самого пакета происходит движение максимумов внутри пакета (рис. 1.8). Максимумы перемещаются со скоростью V, а пакет в целом – со скоростью u.

Там, где фазы совпадают, наблюдается усиление амплитуды, при несовпадении фаз волны гасятся (результат интерференции).

Групповая скорость u может отличаться от фазовой скорости V. Она

может быть больше фазовой скорости, меньше ее или равной ей. В диспергирующей среде u ≠ V.

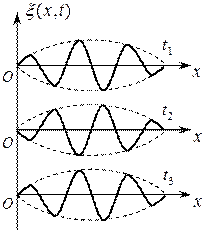Рис. 1.8

Рассмотрим суперпозицию двух волн с одинаковыми амплитудами, распространяющихся в направлении оси OX с начальными фазами, равными нулю.

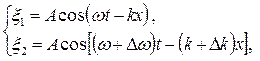(1.7)

где k = ω/V₁; (k + ∆k) = (ω + ∆ω)/V₂ .

Пусть 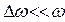, соответственно .

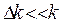При сложении этих волн получаем

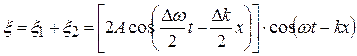. (1.8)

Здесь 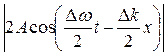– амплитуда результирующей волны, а выражение (1.8) – уравнение плоской волны с медленно изменяющейся амплитудой. В данном случае имеется ряд одинаковых максимумов амплитуды, определяемых условием

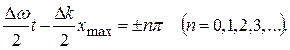(1.9)

Каждый из этих максимумов рассматривается как центр соответствующей группы волн. Разрешив выражение (1.9) относительно 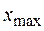, получим:

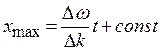, (1.10)

отсюда следует, что

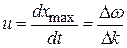, (1.11)

т.е. максимумы амплитуды результирующей волны перемещаются со скоростью u. Выражение (1.11) представялет собой групповую скорость для случая, когда группа волн образована двумя составляющими.

Для волнового пакета, состоящего из нескольких волн, мало отличающихся друг от друга по частоте, выражение (1.11) в пределе примет вид:

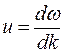. (1.12)

Выражению (1.12) для групповой скорости можно придать другой вид. Заменив ω через Vk, представим (1.12) следующим образом

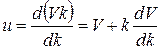. (1.13)

Далее напишем

.

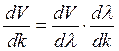Из соотношения 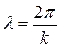вытекает, что 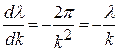. Соответственно 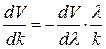. Подставив это значение в (1.13), получим

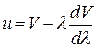. (1.14)

Из этой формулы видно, что в зависимости от знака 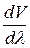групповая скоростьu может быть как меньше, так и больше фазовой скорости V.

В отсутствие дисперсии 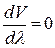, тогда групповая скорость совпадает с фазовой.

Следует также отметить, что для акустических и электромагнитных волн в средах с резонансным поглощением, а также в средах с периодической структурой (кристаллы) возможна даже ситуация, при которой групповая скорость u направлена противоположно фазовой.

Групповая скорость определяет скорость и направление переноса энергии волнами. Понятие групповой скорости играет важную роль и в физике, и в технике, поскольку все методы измерения скоростей распространения волн дают групповую скорость. Именно эта скорость фигурирует при измерении дальности в гидролокации, радиолокации, при зондировании атмосферы, при управлении космическими объектами, в теории связи и т.д.

Однако понятие групповой скорости в средах с сильным поглощением энергии волны неприменимо. Для таких сред вводят величину, характеризующую скорость переноса энергии.

Среды, в которых волны не поглощаются, называются прозрачными. В таких средах групповая скорости и скорость переноса энергии совпадают.

Стоячие волны.Волны называются когерентными, если они имеют одинаковую частоту, разность их фаз не изменяется во времени. При сложении двух или нескольких когерентных волн, в разных точках среды, получается усиление или ослабление результирующей волны. Это явление называется интерференцией волн. Одним из примеров сложения волн служит наложение двух плоских волн, бегущих вдоль оси Оx в среде без затухания в противоположных направлениях с одинаковыми амплитудой и частотой.

Выберем начало координат в точке, в которой обе волны имеют одинаковую начальную фазу, а отсчет времени начнем с момента, когда начальные фазы обеих волн равны нулю, т.е. ξ₁ (x,t) =Asin(wt – kx), ξ₂(x,t)= Asin(wt +kx).

В этом случае результирующее смещение определяется формулой

ξ (x,t) =Asin(wt – kx)+Asin(wt +kx)=2Asinwt∙ coskx=B(x) sinwt,(1.15)

которая является уравнением стоячей волны.

Такое сложение мы можем наблюдать при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная, накладываясь друг на друга, образуют стоячую волну. Из (1.15) видно, что в каждой точке этой волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда В зависит от координаты х:

В(х) = 2А cos kx = 2Acos2px/l.

В тех точках, где 2px/l = np (n = 0,1,2,...), амплитуда В достигает максимума, равного 2А. Эти точки называются пучностями стоячей волны. Координаты пучностей равны

х_nуч = ±nl/2.

В точках, где 2pх/l = ±(n+1/2)p, амплитуда В обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов равны

x_yз = ±(n ±½)l/2.

Из формул для координат узлов и пучностей следует, что расстояние между соседними узлами (так же как и соседними пучностями) равно l/2.

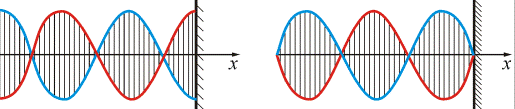
На границе раздела сред, где происходит отражение волны, может возникнуть узел или пучность, это зависит от соотношения плотностей сред. Если среда, от которой происходит отражение, менее плотная, то в месте отражения возникнет пучность (рис.1.9а), если более плотная – узел (рис.1.9б).

а) б)

Рис. 1.9

Образование узла связано с тем, что волна, отражаясь от более плотной среды, меняет фазу на противоположную и у границы раздела сред происходит сложение колебаний с противоположными фазами, в результате чего получается узел. Если же волна отражается от менее плотной среды, то фаза не измененяется и у границы раздела сред колебания складываются с одинаковыми фазами, в результате чего образуется пучность.

В случае стоячей волны переноса энергии колебаний нет, так как падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях. Поэтому полная энергия колебаний частиц среды результирующей стоячей волны, заключенной между узловыми точками, остается постоянной.