Вопрос 3. Методы наблюдения интерференции света.

Впервые интерференционную картину от двух источников света наблюдал в 1802 году английский ученый Юнг. В опыте Юнга (рис.7.3 а, б) источником света служит ярко освещенная щель S, от которой световая волна падает на две равноудаленные щели S₁ и S₂, являющиеся двумя когерентными источниками света (две цилиндрические волны). Интерференционная картина наблюдается на экране Э, расположенном на некотором расстоянии Lпараллельно S₁S₂. Начало отсчета выбрано в точке 0, симметричной относительно щелей.

Усиление и ослабление света в произвольной точке Р экрана зависит от оптической разности хода лучей D =nr₂ - nr₁ = L₂ - L₁. Для получения различимой интерференционной картины расстояние между источниками S₁S₂ = d должно быть значительно меньше расстояния L от источников до экрана.

Расстояние х на экране, в пределах которого образуются интерференционные полосы, значительно меньше L. При этих условиях можно положить, что r₂ + r₁ ≈ 2L.

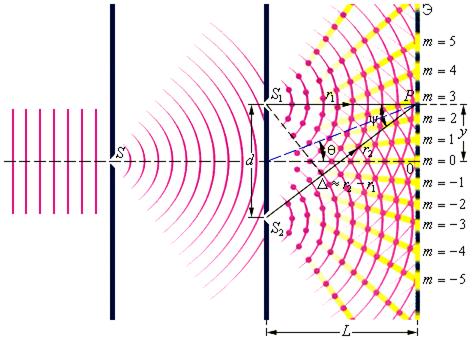
Рис.7.3, а.

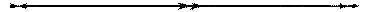
Рис.7.3, б.

Из рис.7.3 б по теореме Пифагора имеем

r ₂² = L² + (x +d/2)²; r ₁² = L² + (x - d/2)²,

откуда r ₂² - r ₁² = 2xd, а

r ₂ – r ₁ » xd/L.

Умножив это выражение справа и слева на показатель преломления среды n, получим

D = nxd/L. (7.6)

Подставив (7.6) в (7.4) получим, что максимумы интенсивности будут наблюдаться при значениях х, равных

х_max = ± mLl/d, (m = 0, 1,2,.,,.). (7.7)

Здесь l = l₀/n - длина волны в среде, заполняющей пространство между источниками и экраном.

Координаты минимумов интенсивности будут:

х_min = ±(m +1/2)Ll/d, (m = 0,1,2,...). (7.8)

Расстояние между двумя соседними максимумами интенсивности называется расстоянием между интерференционными полосами,а расстояние между соседними минимумами - шириной интерференционной полосы.Из (7.7) и (7.8) следует, что расстояние между полосами и ширина полосы не зависят от порядка интерференции (величины m), являются постоянными для данных условий эксперимента L,l,d и имеют одинаковое значение, равное

Dх = Ll/d. (7.9)

Измеряя параметры, входящие в (7.9), можно экспериментально определить длину волны оптического излучения l. Согласно (7.9) Dх пропорционально L/d, поэтому чтобы интерференционная картина была четко различима, необходимо соблюдение упоминавшегося выше условия: d << L. Главный максимум, соответствующий m = 0, проходит через точку 0. Вверх и вниз от него на равных расстояниях друг от друга располагаются максимумы и минимумы интенсивности первого (m =1), второго (m = 2) порядков и т.д., которые представляют собой чередующиеся светлые и темные полосы, параллельные друг другу.

Такая картина справедлива при освещении экрана монохроматическим светом (l₀ = const). При освещении белым светом интерференционные максимумы и минимумы для каждой длины волны будут, согласно формуле (7.9), смещены друг относительно друга и будут иметь вид радужных полос. Только для главного максимума максимумы для всех длин волн совпадают, и в середине экрана будет наблюдаться светлая полоса, по обе стороны от которой симметрично расположатся спектрально окрашенные полосы максимумов первого, второго порядков и т д. Ближе к центральной светлой полосе будут находиться зоны фиолетового цвета, а дальше – зоны красного цвета.

Интенсивность интерференционных полос не остается постоянной, а изменяется вдоль экрана по закону квадрата косинуса.

Наблюдать интерференционную картину можно также с помощью зеркала Френеля, рис 7.4. Бизеркало Френеля состоит из двух плоских зеркал, расположенных под углом, близким 180⁰.

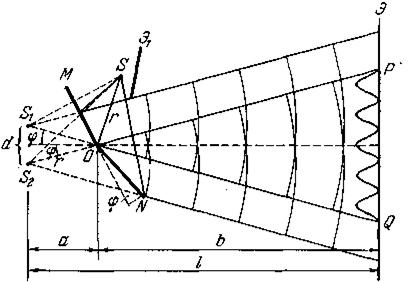
Рис. 7.4.

Свет от источника S падает расходящимся пучком на бизеркало, отражается зеркалами МО и ОN и представляет собой две системы когерентных волн, как бы исходящих из источников S₁ и S₂ , являющихся мнимыми изображениями источника S в зеркалах МО и ОN. Мнимые источники S₁ и S₂ взаимно когерентны, и исходящие из них световые волны приходят в различные точки экрана Э с некоторой разностью фаз, определяемой различием в длине пути от источников r₁ и r₂ до соответствующей точки экрана, и интерферируют. Освещенность экрана в разных точках будет различной. Интерференционная картина будет тем шире, чем меньше угол между зеркалами, а экран должен быть расположен достаточно далеко от зеркала. Прямые лучи от источника света S не доходят до экрана, так как их задерживает заслонка Э₁.

Бипризма Френеля (рис.7.5) состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами α.

Свет от источника S преломляется в обеих призмах, в результате за призмой распространяются световые волны, исходящие как бы из двух мнимых источников света S1 и S2, являющихся когерентными. На достаточно удаленном от призмы экране MN происходит наложение и интерференция когерентных световых волн (участок АВ).

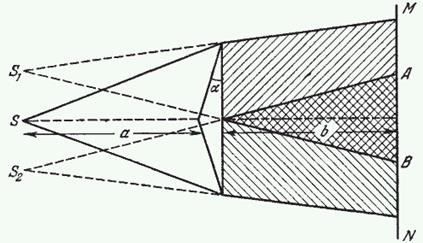
Рис. 7.5

Наблюдать интерференционную картину можно также с помощью зеркала Лойда, билинзы Бийе и других оптических устройств, а также при отражении света от тонких прозрачных пленок, например, от мыльных пленок или от пленок бензина на поверхности воды.

Контрольные вопросы:

1. Как определяется интенсивность световой волны?

2. Какие волны называются когерентными?

3. Что такое интерференция волн?

4. Какую величину называют временем когерентности? Длиной когерентности?

5. Что такое оптическая длина пути? Оптическая разность хода?

6. Какие существуют способы получения когерентных волн?