Вопрос 3. Построение изображений предметов с помощью тонкой линзы.

Оптическая система (в частности линза) лишь в идеальном случае (параксиальные лучи, n = const, λ = const) будет давать изображение светящейся точки в виде точки. Такое изображение называется стигматическим. В реальных оптических системах эти условия не выполняются, в них возникают искажения изображения, называемые аберрациями (или погрешностями). Различают сферическую аберрацию, кому, дисторсиюихроматическую аберрацию. Реальные оптические системы обладают также астигматизмом(погрешностью, обусловленной неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка), т.е. изображение светящейся точки, полученное с помощью такой системы, имеет вид пятна эллиптической формы или отрезка линии. Для уменьшения этих искажений собирают группы линз, называемых оптической системой.Оптическая сила составной системы равна алгебраической сумме оптических сил отдельных линз:

D_{опт. сист.} = ∑D_i.

Важным параметром линзы является линейное или поперечное увеличение Y (масштаб изображения), равное отношению линейных размеров изображения Н к размерам предмета h:

Y = 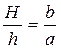. (6.14)

Увеличение положительно для мнимых изображений (изображение прямое), и отрицательно, если изображение предмета перевернутое (действительное изображение). Для плоского зеркала Y = 1, т.е. изображение прямое и натуральной величины.

Кроме линейного увеличения оптическую систему можно также характеризовать угловым увеличением W, равным отношению тангенсов углов φ₂ и φ₁ (рис.6.1), т.е.

W = tg φ₂ /tg φ₁ = a/b. (6.15)

Существует простая связь линейного и углового увеличений. Если предмет и изображение находятся в одной среде, то

Y W = 1. (6.16)

Угловое и линейное увеличения оптической системы различны для разных точек оси, и чем больше линейное увеличение, тем меньше угловое.

Построение изображения предмета в тонких линзах осуществляется с помощью следующих лучей:

1)луча, проходящего через оптический центр линзы и не изменяющего своего направления;

2) луча, идущего параллельно главной оптической оси; после преломления в линзе этот луч (или его продолжение) проходит через второй фокус линзы;

3) луча (или его продолжения), проходящего через первый фокус линзы; после преломления в ней он выходит из линзы параллельно ее главной оптической оси.

Примеры построения изображений объектов, удаленных на разные расстояния от собирающей линзы даны на рисунке 6.6.

Рис. 6.6

Пользуясь описанными геометрическими приемами построения изображений предметов с использованием пересечении лучей, можно проследить, каким будет получаться изображение при различных взаимных положениях объекта и линзы.

1-й случай. Предмет удален в бесконечность влево от линзы, в пространство предметов вдоль оптической оси (рис. 6.6, а). Лучи, идущие от бесконечно удаленной точки, параллельны между собой и пересекутся в главном фокусе линзы. Поэтому бесконечно удаленный предмет, как бы велик он ни был по абсолютным размерам, изобразится в виде точки. Масштаб изображения будет бесконечно мал.

Изображение в этом случае будет построено в задней главной фокальной плоскости, т. е. расположено на главном фокусном расстоянии

от линзы. Практическим примером такого случая построения изображений служит изображение звезды при съемке звездного неба ночью. Лучи, идущие от звезды, можно считать параллельными. Поэтому звезда изобразится на снимке точкой. При этом наиболее резкое изображение получится в главном фокусе. Поэтому при съемке очень удаленных объектов нет необходимости фокусировать изображение, достаточно установить фотоприемник на главном фокусном расстоянии от объектива. В современных системах для регистрации изображений объектов вместо фотопленки используют многоэлементные матричные фотоприемники.

2-й случай. Предмет расположен на конечном расстоянии от линзы, но не ближе удвоенного фокусного расстояния от нее (рис. 6.6, б). Этот случай чаще всего встречается в фоторафической практике и, как уже говорилось, дает уменьшенное обратное действительное изображение объекта. Масштаб имеет конечную величину, меньшую единицы.

Изображение располагается между одинарным и двойным фокусным расстоянием линзы. Чем дальше удален объект от линзы, тем ближе к главному фокусу получается его изображение в пространстве изображений. Чем ближе к линзе расположен предмет, тем дальше от линзы удаляется его изображение (рис. 6.6, б - г).

3-й случай. Если предмет находится на расстоянии, равном удвоенному фокусному расстоянию от линзы (рис. 6.6, в), то получим

равное обратное действительное изображение, удаленное от линзы также на двойное фокусное расстояние. На практике такой случай используют при репродукционных работах, когда нужно получить копию чертежа или рисунка в натуральную величину.

4-й случай. Если предмет находится между двойным и одинарным фокусным расстоянием от линзы (рис. 6.6, г), то изображение будет увеличенным обратным действительным; масштаб изображения больше единицы.

На практике этот случай называется макросъемкой и используется при фотографировании очень мелких предметов, например насекомых, цветов и листьев, деталей мелких механизмов и т. д. Съемка в этом случае возможна только с помощью специальных приспособлений, позволяющих удалить объектив от пленки на расстояние большее, чем удвоенное фокусное.

5-й случай. Предмет находится в главном переднем фокусе линзы (рис. 6.6, д), то его изображение получится в бесконечном удалении от линзы. Масштаб изображения равен бесконечности. Этот случай на практике не используется.

6-й случай. Предмет располагается от линзы на расстоянии меньшем, чем фокусное расстояние (рис. 6.6, е). В этом случае невозможно получить действительное изображение. Поэтому в фотографической практике объекты никогда не размещают на расстоянии, меньшем, чем фокусное расстояние объектива. Однако если в пространстве изображений будет находиться глаз наблюдателя, то ему будет казаться, что лучи исходят не из точки А, а из точки, в которой пересекаются лучи, продолженные влево, в пространство предметов, и он увидит увеличенное прямое, но мнимое изображение предмета, сфотографировать которое нельзя. Такое изображение можно наблюдать, рассматривая мелкие объекты в обычную лупу, где оно будет увеличенным, прямым.

С помощью одной рассеивающей линзы получается мнимое изображение предмета (рис. 6.7), в данном случае прямое уменьшенное, но нельзя получить действительное изображение и сфотографировать его. Однако значение рассеивающих линз различной формы очень велико, так как комбинация их с собирающими линзами позволяет исправлять недостатки (аберрации) объективов и тем самым улучшать качество изображения.

Рис.6.7

Рассеивающие линзы позволяют также изменять фокусное расстояние объектива, а, следовательно, и масштаб изображения.

Контрольные вопросы:

1. Что мы называем главной оптической осью преломляющей сферической поверхности?

2. Какие лучи называются параксиальными?

3. Что называется оптической силой преломляющей сферической поверхности?

4. Что мы называем главными фокусами преломляющей сферической поверхности?

5. Что такое фокальная плоскость линзы?

6. Запишите формулу тонкой линзы?

7. Что называется оптической силой линзы? В каких единицах измеряется оптическая сила линзы?

8. Дайте определение собирающей и рассеивающей линз.

9. Какие лучи используются для построения изображения предмета в тонких линзах?