Вопрос 1. Основные законы геометрической оптики.

Геометрическая оптика это раздел оптики, в котором изучаются законы распространения света в прозрачных средах и построение изображений в оптических системах на основе представлений о световых лучах. Под световым лучом понимают линию, вдоль которой распространяется поток световой энергии. Световой луч является абстрактным математическим понятием, а не физическим образом. На практике обычно используют оптические пучки с шириной значительно большей длины волны, а угловым расширением пучков, связанным с явлением дифракции света на оптических неоднородностях, пренебрегают. Это допустимо, если длина световой волны λ→ 0. Поэтому приближения геометрической оптики можно определить как предельный случай волновой оптики при λ→ 0.

Еще до установления природы света были известны принципы прямолинейного распространения света и независимости распространения световых лучей, законы отражения и преломле­ния света.

Принцип прямолинейного распространения света: свет в оптически однородной среде распространяется прямолинейно. В неоднородной среде, показатель преломления которой является функцией координат, луч искривляется. В этом случае истинная траектория луча может быть найдена на основе принципа Ферма: действительным путем распространения света является путь, для прохождения которого свету требуется минимальное время по сравнению с другими возможными путями между теми же точками.

Согласно принципу независимости распространения световых лучейлуч света при встрече с другими лучами продолжает распространяться в том же направлении, не изменяя амплитуды, частоты, фазы и плоскости поляризации электрического вектора световой волны. Эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Разбивая световой пучок на отдельные световые пучки, можно показать, что действие выделенных световых пучков независимо. Этот закон справедлив лишь при не слишком больших интенсивностях света, когда не играют существенной роли эффекты, связанные с откликом среды на распространение светового луча. При интенсивностях, достигаемых с помощью лазеров, независимость световых лучей перестает соблюдаться.

Если световой луч падает на границу раздела двух прозрачных сред, то в точке падения он разделяется на два луча – отраженный и преломленный, направления которых задаются законами отражения и преломления света.

Закон отражения света: отраженный от границы раздела двух сред луч ІІ лежит в одной плоскости с падающим лучом І и перпендикуляром (штриховая линия), проведенным к границе раздела в точке падения; угол отражения равен углу падения (γ = α), рис.5.1.

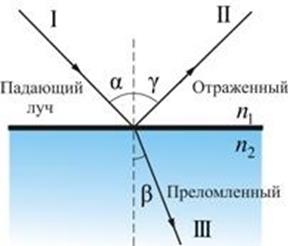
Рис.5.1

Закон преломления света: луч падающий І, луч преломленный ІІІ

и перпендикуляр, проведенный к границе раздела в точке падения (вертикальная штриховая линия), лежат в одной плоскости (рис. 5.1); отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред

sinα/sinβ = n₂₁ = n₂/ n₁ , очевидно sinα/sinβ = V₁/ V₂, (5.1)

где n₂₁ – относительный показатель преломления второй среды относительно первой; V₁ и V₂ – скорости света в первой и второй средах. Относительный показатель преломления двух сред равен отношению их абсолютных показателей преломления n₂₁ = n₂/ n₁, причем показатель преломления первой среды относительно второй n₁₂ равен обратному значению показателя преломления второй среды относительно первой n₂₁.

Абсолютным показателем преломления среды называется величина n, равная отношению скорости с распространения электромагнитных волн в вакууме к их фазовой скорости V в среде:

n = с/ V.

Среда с большим оптическим показателем преломления называется оптически более плотной. При переходе света из оптически менее плотной среды в более плотную получается, что sinα > sinβ, т.е. угол преломления меньше угла падения света.

Из симметрии выражения (5.1) вытекает обратимость световых лучей, сущность которой состоит в том, что если направить световой луч из второй среды в первую под углом β, то преломленный луч в первой среде выйдет под углом α.

При переходе света из оптически более плотной среды в менее плотную при увеличении угла падения угол преломления увеличивается в большей мере (рис. 5.2а, б, в), так что при некотором предельном угле падения α_пр угол преломления становится равным π/2 (рис. 5.2г).

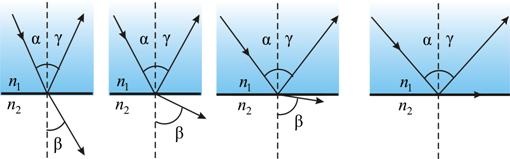
а б в г

Рис. 5.2

С помощью закона преломления можно рассчитать значение предельного угла падения:

sin α_пр /sin(π/2) = n₂₁= n₂/n₁, откуда α_пр = arcsin n₂/n₁. (5.2)

В этом предельном случае преломленный луч скользит по границе раздела сред. При углах падения α > α_пр свет не проникает в глубь оптически менее плотной среды, весь падающий свет полностью отражается, имеет место явление полного внутреннего отражения. Угол α_пр называется предельным угломполного внутреннего отражения.

Явление полного внутреннего отраженияиспользуется в призмах полного отражения, которые применяются в оптических приборах: биноклях, перископах, рефрактометрах (приборах, позволяющих определять оптические показатели преломления), в световодах, представляющих собой тонкие, гнущиеся волокна из оптически прозрачного материала. Свет, падающий на торец световода под углами, большими предельного, претерпевает на границе раздела сердцевины и оболочки полное внутреннее отражение и распространяется только по световедущей жиле. С помощью световодов можно как угодно искривлять путь светового пучка. Для передачи изображений используются многожильные световоды (кабели).

Световоды широко используются в медицине, ЭВМ, интегральной оптике и т.д. Оптические волокна и кабели используются в системах связи для передачи информации со скоростью до 100 Гбит/с. При этом дальность передачи без промежуточных пунктов регенерации сигналов составляет сотни километров.

Для объяснения закона преломления и искривления лучей при прохождении их через оптически неоднородные среды вводится понятие оптической длины пути луча

L = nS или L = ∫ndS,

соответственно для однородной и неоднородной сред, S – геометрическая длина пути луча.

Согласно принципу Ферма для оптической длины пути луча, распространяющегося в неоднородных прозрачных средах, оптическая длина пути луча в среде между двумя заданными точками минимальна, или другими словами, свет распространяется по такому пути, оптическая длина которого минимальна. Поскольку

ΔL = nΔS = (с/V)VΔt = сΔt,

то условие минимума для промежутка времени Δt, который необходим для прохождения света вдоль луча из одной точки в другую, эквивалентно минимуму для оптической длины пути L.