Вопрос 2. Уравнение плоской волны.

<123 4 5 6 7 >

Установим связь между смещением колеблющейся частицы среды (точки) от положения равновесия и временем, отсчитанным от момента начала колебания источника, который находится на расстоянии х от «нашей» частицы в начале координат.

Пусть колебания источника S гармонические, т.е. описываются уравнением ξ(t) = Asinωt. С течением времени все частицы среды также будут совершать синусоидальные колебания с той же частотой и амплитудой, но с различными фазами. В среде возникнет гармоническая бегущая волна.

Частица среды, находящаяся на оси ОХ на расстоянии х от источника S (рис. 1.2), начнёт колебаться позже, чем источник, на время, необходимое, чтобы волна, распространяющаяся от источника со скоростью V, преодолела расстояние х до частицы. Очевидно, что если источник колеблется уже в течение времени t, то частица среды колеблется еще только в течение времени (t – t), где t - время распространения колебаний от источника до частицы.

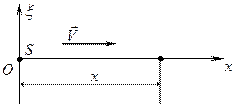Рис. 1.2

Тогда уравнение колебания для этой частицы будет

ξ(x,t) =Asinω(t-τ),

но t =x/V, где V – модуль cкорости распространения волны. Тогда

ξ (x,t) =Asinω(t-x/V)

– уравнение волны.

С учётом того, что 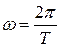и 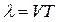, уравнению можно придать вид

ξ (x,t)=Asin2 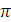(t/T-x/λ) = Asin2 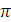(νt -x/λ) = Asin (ωt -2πx/λ) = Asin (ωt -kx),(1.1)

где k = 2p/l – волновое число.Здесь (1.1) – уравнение плоской гармонической монохроматической волны (рис. 1.3), распространяющейся в направлении оси ОХ. График волны внешне похож на график гармонического колебания, но по существу они различны.

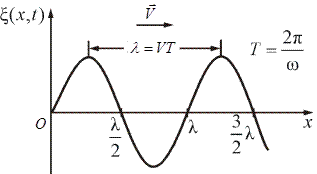Рис. 1.3

График колебания – зависимость смещения данной частицы от времени. График волны – смещение всех частиц среды в данный момент времени на всем расстоянии от источника колебаний до волнового фронта. График волны является как бы моментальной фотографией волны.

Уравнение бегущей волны, распространяющейся в произвольном направлении, имеет вид:

ξ(x,y,z,t) = Asin 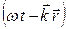= Asin(ωt – k_xx – k_yy – k_zz), (1.2)

где ξ – мгновенное смещение колеблющегося элемента среды (точки) с координатами x, y, z; А – амплитуда смещения; ω – круговая частота колебаний;

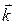– волновой вектор, равный 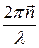( 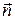– единичный вектор, указывающий направление распространения волны); 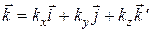; 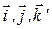- орты;

λ – длинна волны (рис. 1.3), т.е. расстояние, на которое распространяется волна за время, равное периоду колебаний частиц среды; 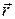– радиус-вектор, проведённый в рассматриваемую точку, ;

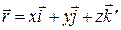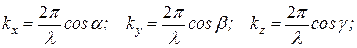
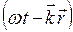– фаза волны, где .

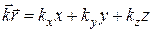Здесь – углы, составленные волновым вектором 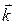с соответствующими осями координат.

Если волна распространяется в среде, не поглащающей энергию, то амплитуда волны не изменяется, т.е. А = const.

Скорость распространения волнового движения является скоростью распространения фазы волны (фазовая скорость). В однородной среде скорость волны постоянна. Если фазовая скорость волны в среде зависит от частоты, то такое явление называется дисперсией волн, а среда – дисперсирующей средой.

При переходе из одной среды в другую может меняться скорость распространения волн, так как меняются упругие свойства среды, однако частота колебаний, как показывает опыт, остается неизменной. Это значит, что припереходе из одной среды в другую будет меняться длина волны l.

Если мы возбудили колебания в какой-либо точке среды, то колебания передадутся всем окружающим ее точкам, т.е. колебаться будет совокупность частиц, заключенных в некотором объеме. Распространяясь от источника колебаний волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к некоторому моменту времени t, называется фронтом волны.

Таким образом, фронт волны является той поверхностью, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть различной формы. Простейшие из них имеют форму сферы или плоскости. Волны, имеющие такие поверхности, называются соответственно сферическими или плоскими.

Часто при решении задач о распространении волн надо строить волновой фронт для некоторого момента времени по волновому фронту, заданному для начального момента времени. Это можно сделать, используя принцип Гюйгенса, сущность которого в следующем.

Пусть волновой фронт, перемещающийся в однородной среде, занимает в данный момент времени положение 1 (рис. 1.4). Требуется найти его положение через промежуток времени Dt.

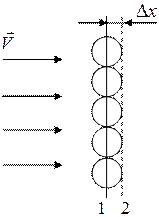Рис. 1.4

В соответствии с принципом Гюйгенса, каждая точка среды, до которой дошла волна, сама становится источником вторичных волн (первое положение принципа Гюйгенса).

Это значит, что от нее, как из центра, начинает распространяться сферическая волна. Чтобы построить вторичные волны, вокруг каждой точки исходного фронта опишем сферы радиусом Dx = VDt, где V –скорость волны. На рис. 1.4 показаны такие сферы. Здесь кружочки – сечения сферических поверхностей плоскостью чертежа.

Вторичные волны взаимно гасятся во всех направлениях, кроме направлений исходного фронта (второе положение принципа Гюйгенса), то есть, колебания сохраняются только на внешней огибающей вторичных волн. Построив эту огибающую, получим исходное положение 2 волнового фронта (штриховая линия). Положения 1 и 2 волнового фронта

− в нашем случае плоскости.

Принцип Гюйгенса применим и к неоднородной среде. В этом случае значения V, а, следовательно, и Dх неодинаковы в различных направлениях.

Так как прохождение волны сопровождается колебанием частиц среды, то вместе с волной перемещается в пространстве и энергия колебаний.

Бегущими волнами называются волны, которые переносят в пространстве энергию и импульс. Перенос энергии волнами характеризуется вектором плотности потока энергии. Направление этого вектора совпадает с направлением переноса энергии, а его модуль называется интенсивностью волны(или плотностью потока энергии) и представляет собой отношение энергии W, переносимой волною сквозь площадь S_┴, перпендикулярную лучу, к продолжительности времени переноса ∆t и размеру площади:

I = W/(∆t∙S_┴),

откуда численно I=W, если ∆t=1 и S_┴=1. Единица интенсивности: ватт на метр в квадрате (Вт/м²).

Получим выражение для интенсивности волны. При концентрации n₀ частиц среды, каждая из которых имеет массу m, объемная плотность w₀энергии складывается из кинетической энергии движения частиц среды и потенциальной энергии, являющейся энергией деформированного объема. Объемная плотность энергии определяется выражением:

w₀ = n₀mw²A²/2 = rw²A²/2,

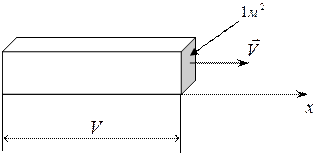
где r =n₀m. Подробный вывод выражения для объемной плотности энергии упругих волн приведен в учебном пособии [13]. Очевидно, за 1с сквозь площадку в 1 м² переносится энергия, содержащаяся в объеме прямоугольного параллелепипеда с основанием 1 м² и высотой, численно равной скорости V (рис. 1.5), следовательно интенсивность волны

I = w₀V = rVw²A²/2. (1.3)

Таким образом, интенсивность волны пропорциональна плотности среды, скорости, квадрату круговой частоты и квадратуамплитуды волны.

Рис. 1.5

Вектор 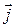, модуль которого равен интенсивности волны, а направление совпадает с направлением распространения волны (и переноса энергии), определяется выражением:

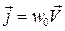(1.4)

и называется вектором Умова.

<123 4 5 6 7 >

Дата добавления: 2017-10-04; просмотров: 2550;