Резонанс напряжений и резонанс токов.
Вопрос 1. Свободные электромагнитные колебания в LC-контуре. Дифференциальное уравнение свободных колебаний и его решение.
Электромагнитными колебаниями в цепи называются периодические изменения во времени значений силы тока и напряжения в электрической цепи, а также обусловленные этим взаимосвязанные колебания электрического и магнитного полей, которые описывают соответственно векторы напряженности электрического 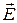 и магнитного
и магнитного 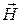 полей. Примером электрической цепи, в которой возникают такие колебания, является электрический колебательный контур, содержащий последовательно соединенные конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R, (рис.2.1).
полей. Примером электрической цепи, в которой возникают такие колебания, является электрический колебательный контур, содержащий последовательно соединенные конденсатор емкостью С, катушку индуктивностью L и резистор сопротивлением R, (рис.2.1).
Если сопротивление R мало (R→0) электрический контур является идеальным (LC – контур). При R≠0 часть электрической энергии будет расходоваться на нагревание проводников и будет наблюдаться затухание колебательных процессов.
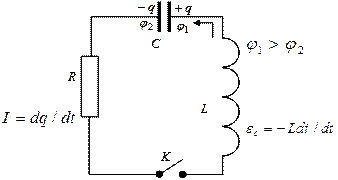
Рис.2.1
Колебания электрического тока в контуре можно вызвать, либо
сообщив обкладкам конденсатора некоторый начальный заряд q, либо возбудив в катушке индуктивности ток. Воспользуемся первым способом. При разомкнутом ключе К зарядим конденсатор С. Между обкладками конденсатора возникнет электрическое поле, энергия которого WC = q2/2C.
После замыкания ключа К конденсатор начнет разряжаться и в контуре потечет электрический ток I. В результате энергия электрического поля будет уменьшаться, но возникнет и начнет увеличиваться энергия магнитного поля, обусловленного током, текущим через индуктивность L. Энергия магнитного поля WL=LI2/2. Если R = 0 (рис. 2.2), то в момент, когда напряжение на конденсаторе, заряд, а следовательно и энергия WC обращаются в нуль, энергия магнитного поля WL и ток достигают наибольшего значения (начиная с этого момента ток течет за счет э.д.с. самоиндукции εс). В дальнейшем ток уменьшается и, когда заряды на обкладках конденсатора С достигнут первоначального значения q (но противоположных знаков), сила тока в цепи станет равной нулю.
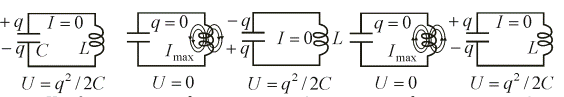
WC = q2/2C WC = 0 WC = q2/2C WC = 0 WC = q2/2C
WL = 0 WL = LI2/2 WL = 0 WL = LI2/2 WL = 0
Рис .2.2
После этого рассмотренные процессы начнут протекать в обратном направлении, контур вернется в исходное состояние и весь цикл повторится снова. Колебания электрического тока (заряда, напряжения)
сопровождаются взаимными превращениями энергий электрического и магнитного полей.
При возрастании электрического заряда на положительно заряженной обкладке конденсатора сила тока в цепи равна
I = dq/dt. (2.1)
Для расчета электрической цепи запишем закон Ома, условившись, что обход контура будем совершать против часовой стрелки:
IR = φ1 – φ2 + εс. (2.2)
Подставив разность потенциалов между обкладками φ2 – φ1 = q/C и э.д.с. самоиндукции εc = –LdI/dt, равенство (2.2) можно переписать в виде дифференциального уравнения второго порядка по отношению к заряду q=q(t) на обкладках конденсатора, и таким образом получить дифференциальное уравнение второго порядка колебаний заряда в контуре:
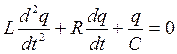 . (2.3)
. (2.3)
Напомним, что дифференциальным уравнением называется уравнение, содержащее искомую функцию, ее производные различных порядков и независимые переменные. Например, в выражении (2.3)
присутствует величина заряда q (искомая переменная функция, зависящая от времени), первая производная этой функции по времени dq/dt и вторая производная этой функции по времени d2q/dt2.
Поскольку внешние э.д.с. в контуре отсутствуют, то рассматриваемые колебания представляют собой свободные колебания.
Если учесть, что R = 0,то процесс периодического превращения энергии электрического поля в энергию магнитного поля и обратно будет продолжаться неограниченно долго, и мы получим незатухающие электрические колебания. Напряжение на обкладках конденсатора меняется во времени по закону U = U0cosω0t, а ток в катушке индуктивности – I = I0cosω0t, т. е свободныеколебания в контуре являются гармоническими с частотой ω0 = 2π/Т0. Используя стандартные обозначения для собственной циклической частоты гармонических колебаний
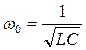 , (2.4)
, (2.4)
уравнение (2.3) перепишем так
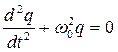 (2.4а)
(2.4а)
– дифференциальное уравнение свободных гармонических колебаний электрического заряда в контуре.
Решением уравнения (2.4а) является функция
q = qmcos(ω0t + α). (2.5)
Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой ω0 (2.4), которая называется собственной циклической частотой контура, т.е. соответствует собственной частоте гармонического осциллятора.
Из (2.4) получаем выражение для периода колебаний (формула Томсона):
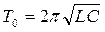 . (2.6)
. (2.6)
Используя известную формулу q = UC и (2.5), запишем выражение для напряжения на конденсаторе:
Uс = (1/C)qmcos(ω0t + α) = Um cos(ω0t + α). (2.7)
Продифференцировав функцию (2.5) по времени, получим выражение для силы тока в контуре:
I = - ω0qm sin(ω0t + α) = Im cos(ω0t + α + π/2). (2.8)
Из (2.8) видно, что сила тока в катушке индуктивности L опережает по фазе напряжение на конденсаторе C на π/2. Сопоставление формул (2.5), (2.7) и (2.8) показывает, что в момент, когда ток достигает наибольшего значения, заряд и напряжение обращаются в нуль, и наоборот, как мы уже это установили ранее, основываясь на энергетических соображениях. Амплитудные значения тока и напряжения:
Um=qm/C, Im = ω0qm, Um = Im 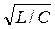 .
.
Дата добавления: 2017-10-04; просмотров: 1619;











