Вопрос 4. Эффект Доплера в акустике.

Механические колебания в интервале частот ν = 16 – 20000 Гц, распространяющиеся в упругой среде, называютсязвуковыми волнами.

Если источник, излучающий звуковые волны с частотой ν₀ = 1/Т₀, и приемник звука (наблюдатель-слушатель) неподвижны относительно среды, в которой распространяются волны, то частота колебаний ν, воспринимаемых приемником, будет равна частоте ν₀ колебаний источника (ν₀ = ν).

Если источник или приемник звука перемещаются в среде друг относительно друга, то частота колебаний, воспринимаемых приемником, изменяется, т.е. ν₀ ≠ ν. Это явление называется эффектом Доплера.

Предположим, что источник и приемник звука движутся вдоль соединяющей их прямой, причем значения скоростей V_ис и V_пр положительны при сближении приемника и источника, и отрицательны при их взаимном удалении.

Сначала рассмотрим случай, когда источник звука приближается со скоростью 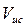к неподвижному наблюдателю (приёмнику). Фазовая скорость Vзвукав среде полностью определяется её упругими и инерционными свойствами и не зависит от состояния движущегося или покоящегося источника. Поэтому относительно среды скорость волны всегда равна V.

За время, равное периоду колебаний 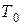, источник приблизится к приёмнику на расстояние .

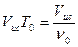Поэтому длина 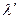волны (рис. 1.10а), распространяющейся в направлении движения источника, будет меньше, чем 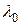, на величину 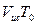, т.е.

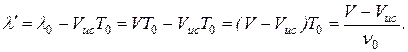(1.16)

Если источник удаляется от приёмника со скоростью 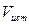(рис. 1.10 б), то длина волны 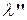, распространяющейся в среде в направлении неподвижного приёмника, будет больше, чем 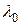, на величину :

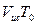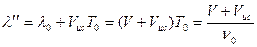. (1.17)

Поскольку частота воспринимаемого приемником звука определяется соотношением 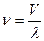, то для обоих случаев (1.16) и (1.17) можем записать 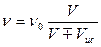. (1.18)

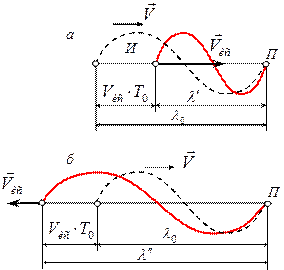Рис. 1.10

Здесь знак «плюс» соответствует удалению источника от приёмника, знак «минус» – приближению к нему.

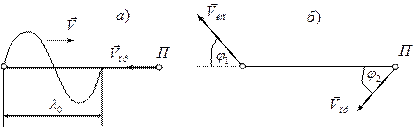Рис. 1.11

В случае если приёмник приближается к неподвижному источнику со скоростью 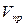(рис. 1.11а), скорость звука относительно приёмника увеличится в соответствии с теоремой сложения скоростей и станет по величине равной 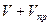. Длина волны от неподвижного источника 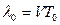, тогда

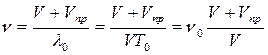. (1.19)

При удалении приёмника в формуле (1.19) вместо знака плюс появится знак минус, и мы сможем записать:

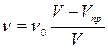. (1.20)

Для обоих случаев, объединив соотношения (1.19) и (1.20), получаем

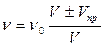. (1.21)

Если источник и приёмник перемещаются одновременно вдоль соединяющей их прямой, то, объединив уравнения (1.18) и (1.21), получим выражение для частоты 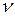, воспринимаемой приёмником звука:

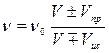. (1.22)

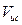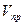В самом общем случае, когда и приемник, и источник звуковых волн движутся относительно среды с произвольными скоростями, направления которых не совпадают с проходящей через источник и приёмник прямой (рис. 1.11,б), в формуле (1.22) вместо значений и нужно брать проекции векторов 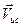и 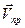на направление указанной прямой. В этом случае формула (1.22) примет вид:

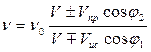. (1.23)

При этом верхние знаки перед скоростям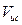и и 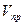берутся в том случае, когда векторы скоростей источника и приёмника (или их проекции) направлены в сторону сближения. Если векторы скоросте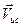й и 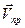(или их проекции) направлены в сторону удаления, следует брать нижние знаки перед соответствующими скоростями.

Разновидностью эффекта Доплера является так называемый двойной эффект Доплера – смещение частоты волн при отражении их от движущихся тел, поскольку отражающий объект можно рассматривать сначала как приемник, а затем как переизлучатель волн.

Доплеровский эффект позволяет измерять скорость движения источников излучения или рассеивающих волны объектов (используется в связи, радио- и гидролокации для измерения скорости движущихся целей). В астрофизике эффект Доплера используется для определения скорости движения звезд и скорости вращения небесных тел. В спектроскопии доплеровское уширение линий излучения атомов и ионов дает способ неконтактного измерения их температуры.