Момент инерции тела

Для тела произвольной формы и массы момент инерции может быть найден суммированием 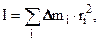где Dm_i – элементарные массы, на которые следует разбить тело при определении его момента инерции, а r_i – расстояние i-того элемента до оси вращения. Для симметричных тел простой формы операция суммирования заменяется интегрированием.

Так как физические тела могут иметь весьма сложную форму и ось вращения может иметь бесконечное множество ориентаций, бессмысленно говорить о величине момента инерции любого тела, как о чем-то фиксированном и навечно застывшем.

При выборе положения оси вращения естественное преимущество отдают осям вращения, проходящим через центр инерции (ЦИ) тела. Пусть выбрана обычная прямоугольная система, с направлениями осей, совпадающими с направлениями геометрической симметрии тела. Для всех тел, кроме простейшего - однородного шара, момент инерции относительно каждой из осей оказывается различным. В общем случае момент инерции тела характеризуется тензором второго ранга (определитель 3´3).

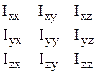, где

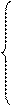
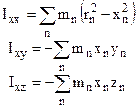
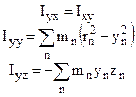
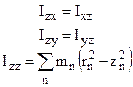
Момент инерции тела относительно оси, проходящей через его ЦИ, называется собственным моментом инерции.

В случае непрерывного распределения массы (без пустот, вырезок, инородных включений и т.п.) компоненты тензора относительно, например, оси y, приобретают интегральный вид

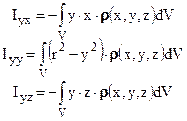
Рассмотрим частные случаи вычисления моментов инерции.