Упругое и неупругое взаимодействия

При взаимодействии тел друг с другом изменяются их энергия и импульс. Это изменение, однако, может происходить по-разному.

Когда речь идет о взаимодействии массивных тел, которые состоят из большого числа частиц, атомов или молекул, имеет смысл наряду с кинетической и потенциальной энергией говорить о внутренней энергии тела. Внутренняя энергия — это энергия всех частиц, составляющих тело, при заданных его температуре и объеме.

В результате взаимодействия тела с другими телами может измениться его температура, а также (необратимым образом) его объем. Ясно, что эти изменения связаны с расходом энергии, т. е. в результате взаимодействия тела с внешними объектами меняется его внутренняя энергия. Такое взаимодействие является неупругим. Оно, очевидно, не сохраняет полной механической энергии тела — суммы кинетической и потенциальной. Напротив, если в результате взаимодействия внутреннее состояние тела не меняется, взаимодействие является упругим. В процессе упругого взаимодействия выполняется закон сохранения механической энергии. Рассмотрим в связи с этими соображениями столкновения двух тел. Столкновение тел заключается в их кратковременном взаимодействии, происходящем при соприкосновении тел. Поскольку вне этого момента времени тела не взаимодействуют, их потенциальная энергия относительно друг друга равна нулю. Взаимодействие при столкновении состоит, таким образом, в передаче от одного тела другому импульса и кинетической энергии. Рассмотрим удар двух шаров, центры которых движутся вдоль одной прямой, т. е. центральный удар. Пусть массы шаров m₁ и m₂, скорости до удара v₁, и v₂, после удара u₁ и u₂. Для определенности возьмем случай движения шаров, изображенный на рис.1.17.

Рисунок 1.17 Центральный удар шаров

Сначала рассмотрим упругий удар шаров. В применении к данной задаче закон сохранения импульса системы шаров имеет вид:

m₁v₁ + m₂v₂ =m₁u₁ + m₂u₂, (1.5)

т.е. импульс системы до столкновения равен импульсу системы после столкновения.

Закон сохранения энергии дает

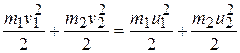. (1.6)

Перенося члены, относящиеся к первому шару влево, а ко второму шару вправо, и разделив одно из полученных уравнений на другое, находим:

, .

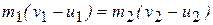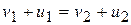Решая полученную систему уравнений совместно, получаем:

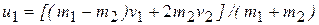, (1.7)

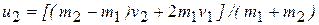. (1.8)

Исследуем полученный результат в частных случаях.

1. Соударение одинаковых шаров. Тогда m₁ = m₂ и

u₁ = v₂, u₂ = v₁. (1.9)

т. е. при упругом центральном ударе двух тел одинаковой массы они просто обмениваются скоростями. Если, в частности, до удара второй шар покоился (v₂ = 0), то после удара остановится первый шар (u₁ = 0), а второй будет двигаться с той же скоростью и в том же направлении, в котором двигался до удара первый шар (u₂ = v₁,).

2. Удар шара о массивную стенку. В этом случае m₂ >> m₁ и приближенно будем иметь:

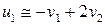(1.10)

.

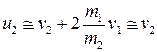Как видно отсюда, скорость массивного тела после удара меняется незначительно. В результате удара стенке передается значительный импульс, но передача энергии при ударе сравнительно мала:

.

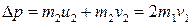Если стенка была первоначально неподвижна (v₂ = 0), то упруго ударившийся о нее шарик малой массы отскочит обратно практически с теми же скоростью (u₁ = ‑ v₁) и энергией.

При ударе о движущуюся стенку происходит обмен энергией между стенкой и шариком тем больший, чем больше скорость стенки. В зависимости от направления движения стенки (v₂ больше или меньше 0) шарик отскакивает от стенки с большими или меньшими, чем до столкновения, кинетической энергией и импульсом.

Рассмотрим теперь абсолютно неупругий удар шаров. При таком ударе энергия налетающего шара полностью расходуется на изменение внутренней энергии другого шара и на сообщение ему некоторой скорости. Закон сохранения механической энергии не выполняется, и для определения скорости после удара достаточно закона сохранения импульса.

m₁v₁ + m₂v₂ =(m₁ + m₂)u₁, (1.11)

откуда

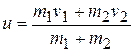. (1.12)

Потеря механической энергии, перешедшей во внутреннюю энергию шаров, равна разности энергий до и после удара:

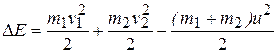. (1.13)

Подставляя сюда (1.12), находим

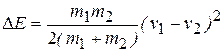. (1.14)

Если ударяемое тело было первоначально неподвижно (v₂ = 0), то

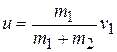(1.15)

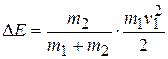(1.16)

Когда неподвижное тело имеет большую массу (m₂ > m₁), то почти вся кинетическая энергия переходит при ударе во внутреннюю анергию. Напротив, при m₁ >> m₂ изменение внутренней энергии мало и большая часть кинетической энергии идет на сообщение движения ударяемому телу.