Момент инерции стержня

Рассмотрим еще пример определения момента инерции тела относительно оси, проходящей через центр масс, но не являющейся осью симметрии. До сих пор мы вычисляли момент инерции относительно оси симметрии; вычисление же момента инерции относительно любой оси, проходящей через центр масс, представляет более сложную задачу. Поэтому рассмотрим сначала самый простой пример: определим момент инерции тонкой палочки длиной l и массы m относительно оси, составляющей с направлением палочки угол a и проходящей через ее центр масс (рис.1.22).

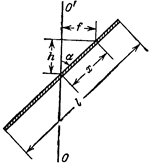
Рисунок 1.22 О моменте инерции стержня

Обозначим через х расстояние от середины палочки какой-то частицы длиной dx. Масса частицы равна 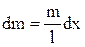и находится она на расстоянии f от оси, f = x×sina. Момент инерции равен

,

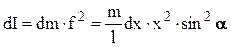а момент инерции всей палочки

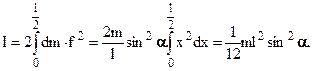(1.22)

Очевидно, если палочка перпендикулярна к оси вращения 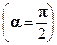, то

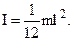(1.23)

Здесь при вычислении момента инерции мы считали палочку очень тонкой, математически это значит, что диаметр сечения палочки имеет бесконечно малую величину, а при обычных приближенных вычислениях мы полагаем, что диаметр палочки ничтожно мал по сравнению с ее длиной.

Теорема Штейнера.

Выше было показано, что момент инерции тела зависит от массы тела и закона распределения этой массы в пространстве, т.е. формы тела. Зависит он также и от положения оси вращения в пространстве.

Если мы каким-либо способом определим момент инерции тела относительно некоторой оси, проходящей через центр масс (собственный момент инерции, обозначаемый I_o), то очень просто определить момент инерции относительно любой параллельной ей оси.

Если момент инерции относительно оси, проходящей через ЦИ, равен I_o, то момент инерции относительно оси, параллельной первичной и проходящей от неё на расстоянии «а», будет равен

I = I_o + ma²,

где I_o – собственный момент инерции,

m – масса тела,

а – расстояние между осями.

Это и есть теорема Гюйгенса-Штейнера, или просто теорема Штейнера.