Момент инерции цилиндра

Момент инерции однородного цилиндра, диска, полого цилиндра и т. п. вычислим относительно его геометрической оси. Любое из этих тел мы можем мысленно разбить на тонкие цилиндрические слои, частицы которых находятся на одинаковом расстоянии от оси. Разобьем цилиндр радиуса R_o на концентрические слои толщиной dR (рис.1.21). Пусть радиус какого-то слоя R; тогда масса частиц, заключенных в этом слое, равна

dm = 2pRhr×dR,

где h – высота цилиндра;

r – плотность вещества цилиндра.

Все частицы слоя будут находиться на расстоянии R от оси, следовательно, момент инерции этого слоя (рис.1.21):

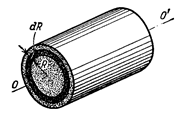
Рисунок 1.21

dI = dm×R² = 2prhR³×dR

Представим, что весь цилиндр разбит на такие слои; тогда момент инерции всего цилиндра будет равен сумме бесконечно малых моментов или момент инерции всего цилиндра

(1.19)

Вспоминая, что масса цилиндра m = pR_o²hr, можно записать так:

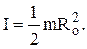(1.20)

Формула (1.20) выражает момент инерции сплошного однородного цилиндра .

Момент инерции полого цилиндра, имеющего внутренний радиус R₁, а внешний R₀ просто вычислить по формуле (1.19), нужно только в интеграле поставить другие пределы, а именно:

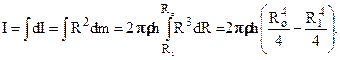
Замечая, что масса полого цилиндра равна 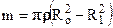, запишем момент инерции полого толстостенного цилиндра так:

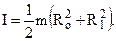(1.21)

Таким же простым путем можно вычислить момент инерции любого тела, которое можно разбить на совокупность полых цилиндров, колец, дисков.