Момент силы, момент импульса
Предположим, что некоторая материальная точка массой m вращается по окружности радиуса r под действием постоянной силы F,ориентированной под некоторым углом a к вектору скорости частицы (иначе движение не будет ни вращательным, ни криволинейным). Разложим силу F на составляющие (рисунок 1.19):
Fn – нормальная составляющая, удерживающая точку m на криволинейной траектории,
Ft – тангенциальная составляющая силы, способная изменить величину скорости движения точки.
Из геометрических соображений
Ft = F×sin a.
С другой стороны, по второму закону Ньютона
Ft = m×at,
здесь аt - линейное тангенциальное ускорение. Из кинематики вращательного движения известно, что аt = e×r.
Итак, можно записать F×sina = m×e×r.
Домножим обе части полученного равенства на r
F×r×sina = mr2×e. (1.17)
Но r×sina = ro – плечо силы F относительно центра вращения О, а произведение силы на её плечо
F×ro = M(1.18)
– момент этой силы относительно оси вращения, в нашем случае проходящей через точку О перпендикулярно рисунку. В векторной форме 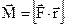 Направление вектора момента силы определяется по известному уже правилу векторного произведения или правого винта.
Направление вектора момента силы определяется по известному уже правилу векторного произведения или правого винта.
Величину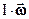 называют моментом импульса тела, а величина
называют моментом импульса тела, а величина 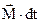 является импульсом момента силы.
является импульсом момента силы.
Общепризнанным является обозначение момента импульса в форме
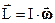 .
.
Понятно, что момент импульса тела – величина векторная, причем направление вектора L точно совпадает с направлением w только если это относится к вращательному движению материальной точки (рис.1.18)
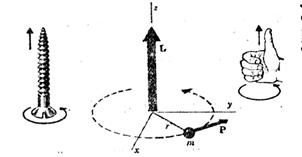 Рисунок 1.18 Определение направления вектора момента импульса – по правилу правого винта. Вы можете выбрать любой удобный для Вас способ определения направлений векторов
Рисунок 1.18 Определение направления вектора момента импульса – по правилу правого винта. Вы можете выбрать любой удобный для Вас способ определения направлений векторов 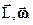 .
.
Из рисунка 1.18 видно также:
1) линия действия вектора Lсовпадает с осью вращения;
2) момент импульса движущейся по окружности материальной точки можно представить как момент вектора ротносительно центра вращения, то есть с плечом r 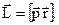
Полученную в (1.17) величину “mr2” обозначают “I” и называют «момент инерции тела массой m, движущейся по криволинейной траектории радиусом r».





 Fn
Fn
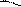

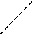 r a Ft
r a Ft
О ro F

Рис1.19. К выводу основного закона динамики вращательного движения
С учетом (1.17) и (1.18) получили, что
M = I×e,
которое называют основным уравнением динамики вращательного движения.
Удобнее это уравнение представить в виде 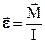 , при этом видно, что уравнение является аналогом уравнения второго закона Ньютона для поступательного движения
, при этом видно, что уравнение является аналогом уравнения второго закона Ньютона для поступательного движения 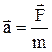 , лишь вместо силы выступает механический момент силы, роль массы m выполняет момент инерции I.
, лишь вместо силы выступает механический момент силы, роль массы m выполняет момент инерции I.
Теперь рассмотрим вращение абсолютно твердого тела произвольной формы относительно произвольной оси, проходящей через любую точку тела (рис.1.20) Разобьем тело на множество элементарных масс. Тогда для каждой из них можно записать выражение, уже полученное нами
Fi×ri×sinai = Dmiri2×e,
где e – угловое ускорение, одинаковое для всех точек тела.
 O
O
 Рисунок 1.20 Вращение тела произвольной формы
Рисунок 1.20 Вращение тела произвольной формы
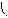







 ri mi
ri mi
a Fi
`
O
Для всего тела тогда можно записать
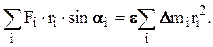
Суммирование по всему объему дает
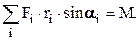
– полный момент сил (относительно оси OO`), действующих на тело.
 – момент инерции тела относительно оси OO`.
– момент инерции тела относительно оси OO`.
Итого получили 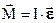 – выражение, аналогичное полученному для материальной точки.
– выражение, аналогичное полученному для материальной точки.
Рассмотрим основной закон динамики вращательного движения поподробнее.
Итак, 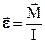 , но, по определению углового ускорения e, его величина равна
, но, по определению углового ускорения e, его величина равна 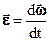 , следовательно,
, следовательно, 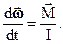
Откуда получаем  . Если I = const, то момент инерции можно внести под знак дифференциала и можно записать
. Если I = const, то момент инерции можно внести под знак дифференциала и можно записать
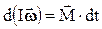
Это выражение иногда называют основным законом динамики вращательного движения в импульсной формулировке, а величина 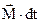 является импульсом момента силы.
является импульсом момента силы.
Общепризнанным является запись основного уравнения динамики вращения в форме
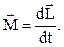
Дата добавления: 2017-10-04; просмотров: 1997;











