Связь силы и потенциальной энергии

Каждой точке потенциального поля сил соответствует, с одной стороны, некоторое значение силы F, действующей на тело, с другой стороны – некоторое значение потенциальной энергии U для данной конфигурации взаимодействующих тел. Следовательно, между 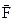и U должна существовать какая-то функциональная связь.

Вычислим элементарную работу dA, совершаемую силами поля при малом перемещении тела 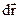вдоль некоторого произвольного направления S.

,

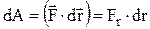где F_r = F×cos a - проекция силы на направление перемещения.

Работа эта совершается за счет запаса потенциальной энергии системы и равна убыли потенциальной энергии (-dU), т.е.

dA = - dU(r) или F_r×dr = -dU.

Откуда 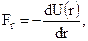или в векторной форме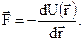

Если отрезок произвольно ориентирован в трехмерном пространстве, то величину силы можно определить параметрически:

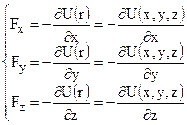
В векторном виде это равенство можно записать еще так

,

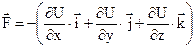где 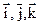- орты осей координат x,y,z.

В математике вектор 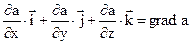называется градиентом скалярной величины «а». Этот вектор направлен в сторону максимально быстрого увеличения скалярной величины «а».

В нашем случае сила (векторная величина) есть градиент потенциальной энергии – величины скалярной. Знак “ – “ указывает, что вектор силы 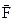направлен в сторону убывания потенциальной энергии U.

Иные обозначения

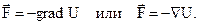
Важное замечание:прибавление постоянной во времени величины к потенциальной энергии не изменяет картины силового воздействия данного силового поля на данную частицу (тело) (вследствие операции дифференцирования).

Следовательно:

а) выбор уровня, с которого производится отсчет величины потенциальной энергии – произвольная операция, допускающая удобный выбор;

б) строго определенный физический смысл имеет не фиксированное значение потенциальной энергии, а её изменение в данном процессе – приращение или убыль.