Третий закон Ньютона

<4 5 678 9 10 >

Третий закон Ньютона имеет дело со взаимодействующими, телами. Он утверждает, что силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению. Важно подчеркнуть, что силы, о которых идет речь, приложены к разным взаимодействующим друг с другом телам.

Уравнения Ньютона обладают тем свойством, что некоторые величины, характеризующие движение частицы, остаются неизменными во все время движения. О таких величинах принято говорить, что они сохраняются. Их также называют интегралами движения. Знание интегралов движения позволяет получить ряд важных следствий без фактического решения уравнений движения. Рассмотрим тело или систему тел в отсутствие внешних сил. Система тел, на которую не действуют внешние силы (или векторная сумма этих сил равна нулю), является замкнутой. В этом случае F = 0; как видно из уравнения (1.1)

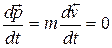, (1.2)

т.е. 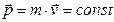величина , остается постоянной во все время движения. Полученный результат представляет собой закон сохранения импульса, который имеет место как для одного тела, так и для системы тел в отсутствие внешних сил.

Закон сохранения импульса пока не опровергнут ни в каких опытах: ни в макроскопической классической физике, ни в микромире, ни при релятивистских скоростях движения.

Для вывода третьего закона Ньютона рассмотрим изолированную систему, состоящую только из двух взаимодействующих тел. Полный импульс такой системы составляет 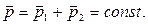. Продифференцируем это уравнение по времени и учтем закон сохранения импульса

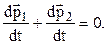
Из второго закона Ньютона

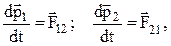
где F₁₂ – сила, действующая со стороны второго тела на первое, а F₂₁ – сила, с которой первое тело действует на второе. Их еще называют силами действия и противодействия.

Мы получили третий закон Ньютона:

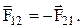
Следует учитывать, что третий закон Ньютона строго выполняется лишь для статических и контактных взаимодействий. Дело в том, что сигнал взаимодействия распространяется с конечной скоростью: в вакууме со скоростью света, в твердом теле – со скоростью продольной волны.

Центр инерции

Импульс замкнутой механической системы имеет различные значения по отношению к различным инерциальным системам отсчета. Если система отсчета K' движется относительно системы K со скоростью V, то скорости частиц v'_α и v_α в этих системах связаны соотношением v_α = v'_α + V . Поэтому связь между значениями P и P' импульса в этих системах дается формулой:

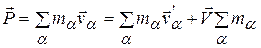
или

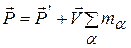
Всегда можно подобрать такую систему отсчета K', в которой полный импульс обращается в нуль. Положив P' =0, находим, что скорость этой системы отсчета

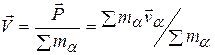. (1.3)

Если полный импульс механической системы равен нулю, то говорят, что она покоится относительно соответствующей системы координат. Скорость Vимеет смысл скорости движения механической системы как целого с отличным от нуля импульсом. Связь между импульсом Pи скоростью Vсистемы как целого такая же, какая была бы между импульсом и скоростью одной материальной точки с массой, равной сумме масс в системе, .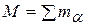

Правая сторона формулы (1.3) может быть представлена как полная производная по времени от выражения:

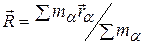(1.4)

Можно сказать, что скорость V системыкак целого есть скорость перемещения в пространстве точки, радиус-вектор которой дается формулой (1.4). Такая точка является центром инерции системы.

Закон сохранения импульса замкнутой системы можно сформулировать как утверждение о том, что ее центр инерции движется прямолинейно и равномерно. Это есть обобщение закона инерции для свободной материальной точки.

<4 5 678 9 10 >

Дата добавления: 2017-10-04; просмотров: 1033;

Третий закон Ньютона

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Публикации по педагогике