Взаимное расположение прямых и плоскостей
2.5.1 Прямые параллельны:
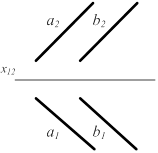
 а || b Û{а1 || b1; а2 || b2} а || b Û{а1 || b1; а2 || b2}
| 
|
Рисунок 2.12
Если две прямые в пространстве параллельны, то и соответствующие проекции этих прямых параллельны и обратно, если соответствующие проекции двух прямых параллельны, и прямые в пространстве параллельны.
Чтобы прямые в пространстве были параллельны, необходимо и достаточно, чтобы соответствующие проекции прямых были параллельны(рис. 2.12) или совпадали (рис 2.13 б).
2.5.2 Прямые пересекаются (рис 2.13 а): а ∩ b = М Û{а1 ∩ b1 = М1; а2 ∩ b2 =М2}. Линия связи М1 М2^ x12.
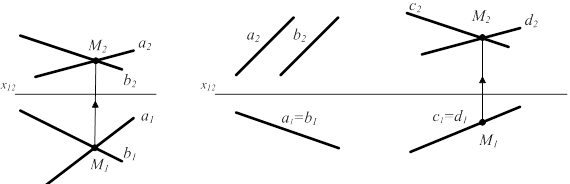
а) aÇb б) a || b в) c∩d
Рисунок 2.13
Если две прямые, параллельные или пересекающиеся, лежат в одной проецирующей плоскости, их изображения на соответствующую плоскость проекций совпадут. Такие прямые называются конкурирующими (рис. 2.13 б, в) – конкурирующие относительно пл. П1.
2.5.3 Прямые скрещивающиеся (рис 2.14).: а ¸ b Û {а1 ∩ b1 =М1; а2 ∩ b2 =N2}
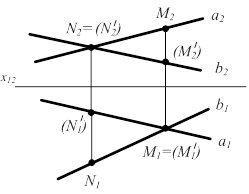
| М и М′ - конкурирующие точки относительно плоскости П1 N и N′ - конкурирующие точки относительно плоскости П2 |
Рисунок 2.14
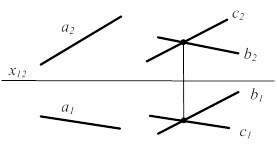
2.5.4 Прямая параллельна плоскости (рис 2.15)
Прямая параллельна плоскости, если она параллельна, хотя бы одной прямой, принадлежащей этой плоскости.
a || å(b ∩ c), если a || c
 т.е. a1 || c1
a2 || c2 т.е. a1 || c1
a2 || c2
| 
|
Рисунок 2.15
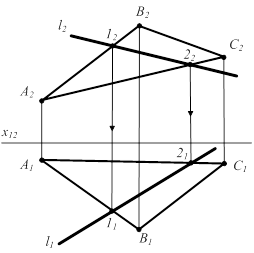
2.5.5 Прямая принадлежит плоскости(рис 2.16)
l Î å(ABC)
l Î (1,2)
 (1,2) Î å(ABC)
1 Î AB (11Î A1B1; 12Î A2B2)
2 Î AC (21Î A1C1; 22Î A2C2) (1,2) Î å(ABC)
1 Î AB (11Î A1B1; 12Î A2B2)
2 Î AC (21Î A1C1; 22Î A2C2)
| 
|
Рисунок 2.16
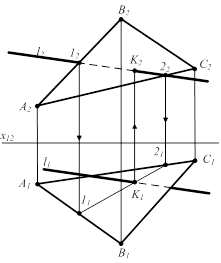
2.5.6 Прямая пересекает плоскость (первая основная позиционная задача) (рис 2.17)
l ∩ å(ABC) =K, т.к.
l и (1,2) конкурирующие прямые и
 (1,2) Î å(ABC), а
l ∩ (1,2) = K
Для определения видимости прямой относительно плоскости необходимо рассмотреть расположение конкурирующих точек l и АВ относительно П2; l и ВС относительно П1. (1,2) Î å(ABC), а
l ∩ (1,2) = K
Для определения видимости прямой относительно плоскости необходимо рассмотреть расположение конкурирующих точек l и АВ относительно П2; l и ВС относительно П1.
| 
|
Рисунок 2.17
Дата добавления: 2017-10-04; просмотров: 1487;











