Взаимная параллельность плоскостей

Построение двух взаимно параллельных плоскостей основано на известном положении, что две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.

Задача: Через точку К(К₁К₂) (рис. 2-31.а) провести плоскость D, параллельную плоскости Г(АВС). Плоскость D задать пересекающимися прямыми.

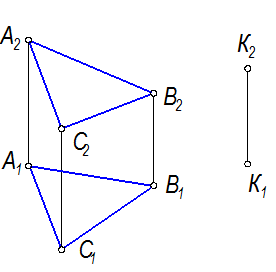
Рис. 2-30

Алгоритм:

1. Плоскость D зададим прямыми m Ç n = K (рис. 2-31).

2. Прямую m возьмём параллельно стороне СВ треугольника. Если m || СВ, то m₁ || C₁B₁, a m₂ || C₂B₂

3. Прямую n возьмём параллельно стороне АВ треугольника. Если n || AB, mo n₁ || A₁B₁, a n₂ || A₂B₂.

4. Таким образом, плоскости S(АВС) и D(m Ç n) параллельны.

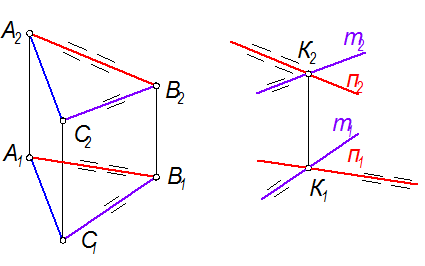
Рис. 2-31

Как вы думаете?

1. Сколько решений может иметь задача, представленная на рис. 2-30?

2. Чем можно ещё задать плоскость D, кроме решения, приведённого на рис. 2-31?

3. Сколько ответов может быть у задачи, представленной на рис. 2-29? Почему?

Выводы:

1. В общем случае плоскость определяют три точки.

2. Общий признак плоскостей частного положения - одна из проекций вырождается в прямую линию.

3. Точку в плоскости находят по принадлежности какой-нибудь прямой этой плоскости.

4. В любой плоскости можно построить прямые уровня и линии наибольшего наклона плоскости к каждой из плоскостей проекций.

5. Через точку, лежащую вне плоскости, можно провести сколько угодно прямых, параллельных данной плоскости, но только одну плоскость, параллельную заданной.

Справочный материал

Примеры изображения плоскостей общего и частного положения, заданные геометрическими фигурами