Прямая или плоскость параллельная профильной плоскости проекций называется профильной прямой или плоскостью.

Для построения чертежа профильной прямой необходимо использовать трехкартинный эпюр (рис.2.7).

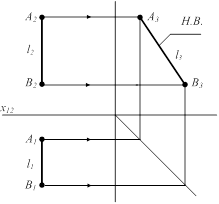
Рисунок 2.7

Прямая или плоскость неперпендикулярная и непараллельная ни одной из плоскостей проекций называются прямой или плоскостью общего положения.

Обе проекции прямой общего положения на комплексном чертеже не параллельны и не перпендикулярны оси чертежа. Чтобы найти Н.В. ее отрезка применяют правило прямоугольного треугольника (рис. 2.8):

Длина отрезка прямой общего положения на чертеже определяется гипотенузой прямоугольного треугольника, один катет которого является одна из проекций этого отрезка, а другой - алгебраическая разность расстояний от концов отрезка до соответствующей плоскости проекций.

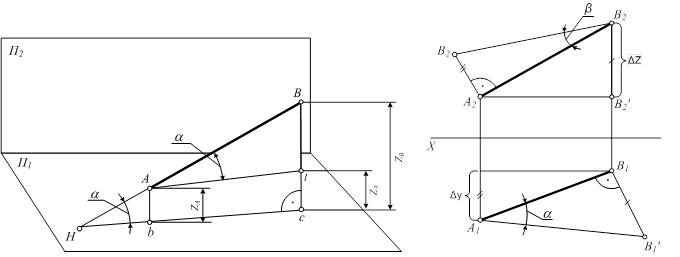
Рисунок 2.8

Точки пересечения прямых с плоскостями проекций называются соответ­ственно горизонтальным(H)и фронтальным(F)следами прямых(рис.2.9).

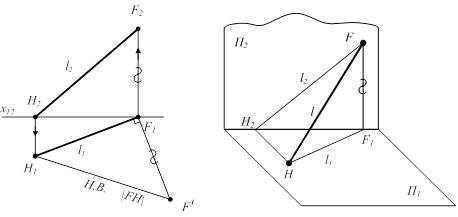
Рисунок 2.9

Линии пересечения плоскостей с плоскостями проекций называются соответственно горизонтальным и фронтальным следами плоскостей(рис.2.10).

Три плоскости П₁, П₂ и плоскость общего положения S пересекаются в одной точке схода следов.

Задание плоскости следами - это частный способ ее задания, разновидность задания плоскости двумя пересекающимися прямыми ®S ( f ∩ h).

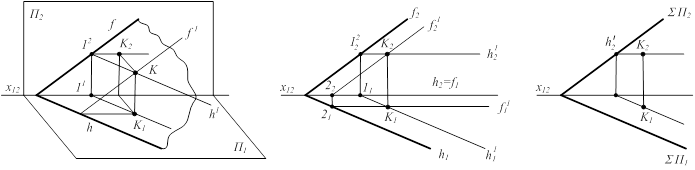
Рисунок 2.10

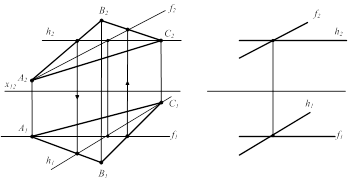
В любой плоскости общего положения всегда можно провести сколько угодно горизонталей и фронталей - главных линий плоскости -(рис.2.11). (К главным линиям плоскости относятся также линии ската – линии, перпендикулярные фронталям и горизонталям плоскости). Все горизонтали (фронтали), лежащие в одной плоскости, параллельны между собой, поэтому часто плоскости задают пересекающимися прямыми f ∩ h или следами.

f Î å(ABC) f1 || x12 h Î å(ABC) h2 || x12 ®S f ∩ h

Рисунок 2.11