Дифференцирующие цепочки – почему их так называют
Сначала определим как "идеально дифференцирующую" такую цепочку, выходной сигнал которой есть производная от входного. Это означает выполнение условия:
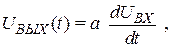
где а – постоянная. (2.22)
Зададимся вопросом: при каких условиях цепочка будет "идеально дифференцирующей"? Подадим на дифференцирующую цепочку (рис. 2.11) импульс напряжения длительностью t2.
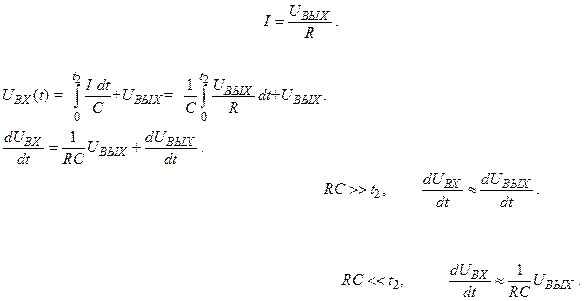 |
Ток через сопротивление R будет Сумма напряжений на конденсаторе и на сопротивлении будет:
Продифференцируем эту сумму по t :
Если постоянная времени цепочки большая то
При таком условии выходное напряжение почти равно входному и цепочка передаёт сигнал с небольшими искажениями.
Если постоянная времени цепочки маленькая то
Выходное напряжение пропорционально производной от входного!
С некоторой погрешностью сигнал на выходе цепочки с небольшой постоянной времени будет продифференцирован.
А Б
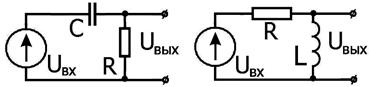 Рис. 2.14.
Рис. 2.14.
Дифференцирующие
цепочки.
Надо сразу подчеркнуть, что "идеально дифференцирующую" цепочку нельзя собрать из R, C, L элементов, это математическая абстракция. Но если идеал недостижим, то к нему можно приблизиться.
Дата добавления: 2017-10-04; просмотров: 1333;











