Пример – дифференцирующая цепочка

На рис. 2.11 показана так называемая дифференцирующая цепочка. Рассчитаем коэффициент передачи этой простейшей RC-цепочки:

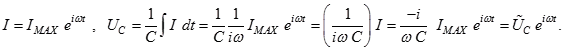
(2.16)

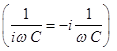Напряжение на конденсаторе Ũ_C пропорционально току. Коэффициент

пропорциональности – это аналог сопротивления для переменного тока. Его

называют импеданс.

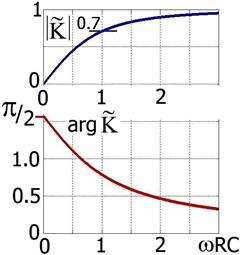
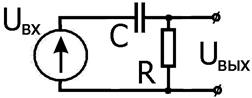
Рис. 2.11.

Дифференцирующая цепочка и её

частотная и фазовая характеристики.

Коэффициент передачи:

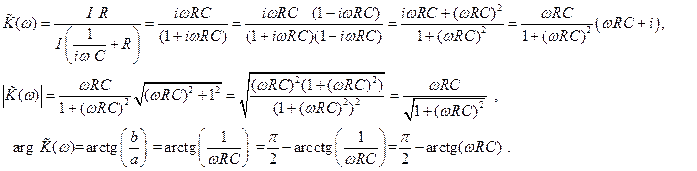
(2.17)

(2.18)

Известно, что при делении комплексных чисел модули делят, а фазы вычитают.

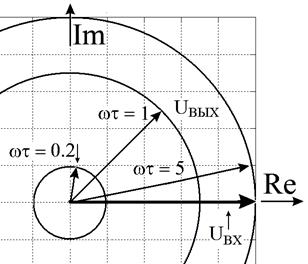
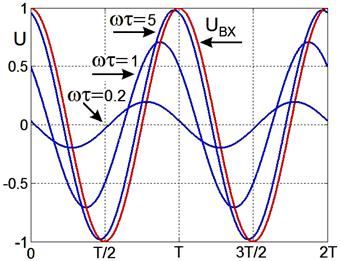
Рис. 2.12.

Входное напряжение U_BX и выходные напряжения на дифференцирующей цепочке, (рис. 2.11), при различных значениях постоянной времени цепочки. τ = RC.

При ωτ = 1 модуль коэффициента передачи равен 0.7, и выходное напряжение отстаёт по фазе от входного на π/4.

При ωτ >> 1 выходное напряжение почти совпадает со входным.

При ωτ << 1 выходное напряжение меньше входного и отстаёт по фазе почти на π/2.

Для той же дифференцирующей RC-цепочки, изображённой на рис. 2.11, мы можем рассчитать переходную характеристику, решая дифференциальное уравнение:

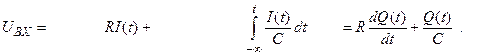
Q – заряд конденсатора.

напряжение
на сопротивлении на конденсаторе

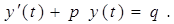Получилось уравнение вида

Чтобы вычислить переходную характеристику h(t) из этого дифференциального уравнения, подадим на вход дифференцирующей цепочки ступеньку.

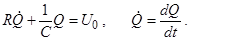
Если U_ВХ (t) = U₀ H(t) , то получится уравнение .

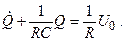
Или

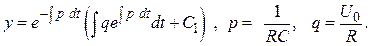Из Бронштейна и Семендяева:

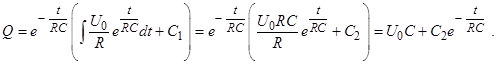
При t = 0, Q = 0, C₂ = – U₀ C .

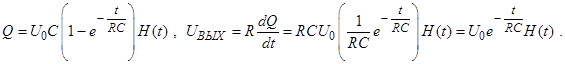(2.20)

(2.21)

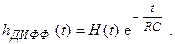Здесь множитель H(t) введён, чтобы учесть отсутствие сигнала для отрицательных времён: h (t < 0) = 0 (принцип причинности).

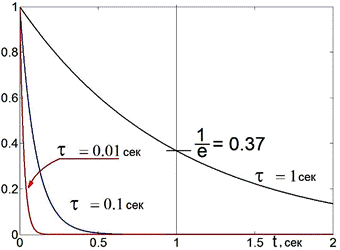
Рис. 2.13.

Переходная функция или переходная характеристика дифференцирующих цепочек с разными постоянными времени. При t = τ = RC экспонента уменьшается в е = 2,718281828 раз.