Условие интегрируемости на частотном языке

Теперь мы можем сформулировать условие интегрируемости на частотном языке, сравнивая выражения (2.30) и (2.31). Видно, что цепочки на рис. 2.16 будут приближённо интегрирующими при выполнении условия:

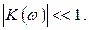
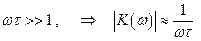
, при условии, что (2.32)

Это означает, что на выходе наших цепочек мы получим интеграл от входного сигнала, если выполняется это условие, т.е. частоты достаточно высокие. Естественно, мы получим интеграл в некотором приближении.

Опять заметим (как и для дифференцирующих цепочек), что для интегрируемости требуется выполнение условия (2.32) для большей части частот Фурье образа входного сигнала, и качество интегрирования будет определяться тем, насколько велика эта часть.

Условие интегрируемости на временно́м языке

Кроме частотного рассмотрения, полезно рассмотреть действие наших интегрирующих цепочек на временно́м языке. Опять в качестве примера рассмотрим прямоугольный импульс длительности t₀, изображённый на рис. 2.15 справа. Прямоугольный импульс можно представить как суперпозицию (наложение) двух ступенек (показаны пунктиром на верхнем графике рис. 2.15).

Сразу отметим, что математически интеграл от такого прямоугольного импульса есть просто линейно-ломаная функция ( U_{ИД ИНТ} на рис. 2.15 справа).

Теперь нетрудно найти выходное напряжение в наших цепочках. Это будут две экспоненты, как показано на рис. 2.15 справа внизу. Причём, если время релаксации τ велико по сравнению с характерным временем процесса, то выходное напряжение похоже на интеграл от сигнала, если τ >> t₀ . (2.33)

Таким образом, мы получили приближённое условие интегрируемости на временном языке. Это условие приложимо к сигналу и произвольной формы, если под t₀ мы будем понимать характерное время сигнала. Особенно наглядно качество интегрирования показано на рис. 2.18. Чем короче прямоугольный импульс, тем меньшую часть экспоненты он отрезает.

Ряд для экспоненты начинается с линейного члена, и если выполняется условие (2.33), то можно ограничиться только этим линейным членом. А интеграл от константы – линейная функция.

Заметим, что условия (2.32) и (2.33) эквивалентны, а применение одного или другого зависит от того, какой язык (частотный или временной) используется в задаче.

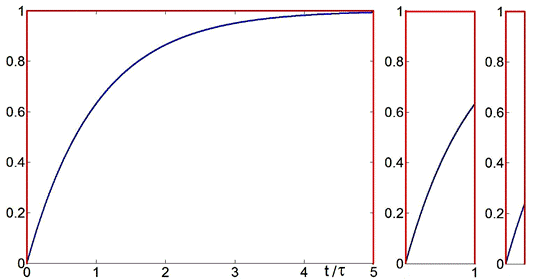
Рис. 2.18.

Части экспоненты.

Большая, поменьше и совсем маленькая.

A B C

На рис. 2.18 изображена реакция интегрирующей цепочки на первый полупериод прямоугольных импульсов разной длительности.

A. При длительности 5 τ напряжение почти выходит на асимптоту.

B. При длительности τ реакция почти похожа на интеграл от константы.

C При длительности 0.25 τ реакция отличается от линейной функции менее чем на толщину линии.