Метод комплексных амплитуд

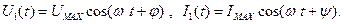Пусть в линейной цепи действуют гармонические источники напряжения U или тока I
на частоте ω .

Тогда установившиеся токи и напряжения будут иметь ту же частоту, но разные фазы. Для расчёта амплитуд и фаз установившихся колебаний применяется символический метод (метод комплексных амплитуд, Ch. P. Steinmetz).

Напомним некоторые формулы из теории комплексных чисел:

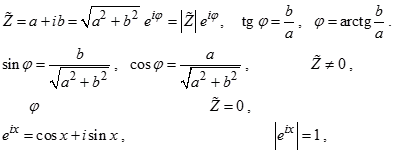
если

не определено, если

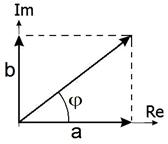
(формула Эйлера), Рис. 2.8.

Значок ~ над числом показывает, что число (или функция) – комплексные.

Метод комплексных амплитуд или символический метод позволяет представить любую колеблющуюся гармонически величину в виде квази-вектора, вращающегося с круговой частотой ω. Тогда любую функцию, зависящую от времени по гармоническому закону, можно представить как действительную часть комплексной экспоненты:

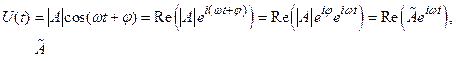
(2.9)

где – комплексная амплитуда, а φ - фаза.

Такие квази-векторы удобно применять для изображения гармонических переменных токов, однако они изображают только амплитуды (своей длиной) и проекции на оси. Направления в пространстве, (в отличие от настоящих векторов), они не указывают.

При такой записи операции дифференцирования и интегрирования (в смысле нахождения первообразной) сведутся к операциям умножения и деления:

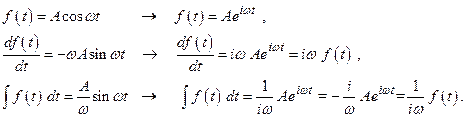
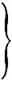
(2.10)

Векторная диаграмма рис. 2.8 – мгновенная картина. При ωt = 0, 2π и т.д. e^iωt = 1. При такой временной зависимости картина будет вращатьсяпротив часовой стрелки с угловой скоростью ω. Это можно представить, если написать, что e^iωt = ,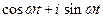
и проследить, как будет меняться синус и косинус с увеличением времени.

Конечно, если зависимость от времени будет e^–iωt , то вращение будет по часовой стрелке.

Это можно увидеть воочию при помощи программки на Матлабе.

(Кстати, написанное мелким шрифтом можно пропускать без ущерба для понимания).

clc; %чистит окно команд

FigureColor=[1,1,1]; hFigure=gcf; set(hFigure, 'Color', FigureColor) %удаляют рамку графика

title('exp(+ i \omega t)','FontSize', 28); %заголовок, omega – круговая частота.

tic;pause(2);toc; %время для прочтения заголовка

for t = 0:0.027:2*pi; axis([-1 1 -1 1]) %границы области графика

x=-sin(t); y=cos(t); h = plot(x,y,'k.'); hold on; pause(0.01)

end; pause(2)

clf; %чистит графическое окно

title({' '; 'exp(– i \omega t)'}, 'FontSize', 28); %заголовок, omega – круговая частота.

tic;pause(2);toc; %время для прочтения заголовка

for t = 0:0.028:2*pi; axis([-1 1 -1 1]) %границы области графика

x=sin(t); y=cos(t);

h = plot(x,y,'ro'); hold on; pause(0.01)

end; pause(1); clf;

Если напряжения и токи в цепи зависят от времени не гармонически, то можно разложить их по гармоническим составляющим в ряд или интеграл Фурье:

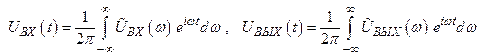
. (2.11)

К этому методу мы ещё вернёмся (см. (3.20), (3.21)).