Анализ линейных систем
Стационарная система – это система, в которой сдвиг входного сигнала во времени приводит к такому же сдвигу выходного сигнала. В общем случае анализ линейной стационарной системы сводится к решению системы линейных дифференциальных (или интегро-дифференциальных) уравнений с постоянными коэффициентами. Такие системы называются линейными и стационарными. Для получения этих уравнений используются известные правила Кирхгофа. Вот они.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю. Узлом называется точка, в которой сходится более чем два проводника. Это правило вытекает из закона сохранения заряда. Число уравнений, составленных по первому правилу Кирхгофа, должно быть на одно меньше, чем число узлов в исследуемой цепи. Этим обеспечивается линейная независимость получаемых уравнений.
Второе правило Кирхгофа: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна сумме всех ЭДС в этом контуре. При составлении уравнений согласно второму правилу Кирхгофа токам и ЭДС нужно приписывать знаки в соответствии с выбранным направлением обхода.
Задача простая, но громоздкая. Например, для схемы на рис. 2.7 получаются следующие уравнения:
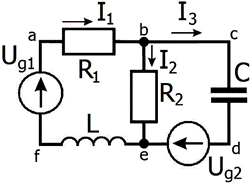
Рис. 2.7.
Схема для демонстрации правил Кирхгофа. На изображениях электрических цепей (на схемах) провода заменяют отрезками прямых. Считают, что провода на схеме имеют нулевое сопротивление.
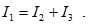
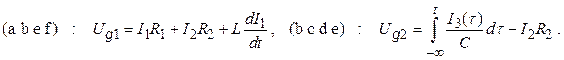
Контур
Решение системы линейных интегро-дифференциальных уравнений обычно громоздко. Чтобы избежать громоздкости применяют различные методы, среди которых на первом месте – метод комплексных амплитуд (для гармонических сигналов). Этот метод позволяет заменить интегро-дифференциальные уравнения на алгебраические.
Для линейных стационарных систем справедлив принцип суперпозиции:
если в цепи есть несколько источников тока или напряжения, то можно рассчитать отклик системы на каждый источник отдельно. Тогда отклик системы в целом будет просто равен сумме отдельно рассчитанных откликов.
Каждый источник не влияет на другие, а работает независимо.
Хотелось бы подчеркнуть, что принцип суперпозиции справедлив только в линейных системах.
Дата добавления: 2017-10-04; просмотров: 1268;











