Оценка величины эффекта

Проблема учета адиабатического нагрева при сжатии образцов далеко не новая. Исследователи решают ее по-разному. Можно варьировать скорость сжатия - при бесконечно малой скорости процесс можно считать изотермическим, но это неудобно из практических соображений. Можно изменять геометрию камеры высокого давления, использовать термостабилизацию ее стенок, что, впрочем, дает незначительный эффект. Можно просто пренебречь нагревом, считая изменение температуры малой по сравнению с начальной температурой обработки. Например, для воды адиабатическая нагрева составляет всего 3°С на 100 МПа, следовательно, на практике под давлением 600 МПа при конечной скорости сжатия температура поднимается не более чем на 18°С, что, конечно, немного по сравнению с начальной температурой Т₀~ 300 К.

Посмотрим, в каких случаях и в какой степени подобное повышение температуры в результате адиабатического сжатия может изменить константу скорости реакции в модели первого порядка. Для этого воспользуемся формулой Аррениуса и изобразим графически (см. Рис. 8.4) относительное изменение константы скорости реакции, имеет вид:

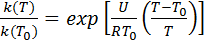(8.3)

В зависимости от величины активационного барьера для случаев Т₀ =300 К, (Т-Т₀)=10, 15 и 20°С. Для дальнейших оценок воспользуемся данными о влиянии высокого давления на инактивацию МАФАМ в вишневом соке: предэкспоненционный множитель в формуле Аррениуса А = ехр (13,52) Гц, 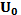=15,9 ккал/моль, ∆V= -35,5 мл/моль (табл. 7.1).

При изменении давления Р от 0 до 600 мпа активационный барьер U=U₀+ Р∆V меняется от 16 до 11 ккал / моль. Поделив эти границы на RТ₀=0,6 ккал/моль, получаем, что характерные значения отношения U/RТ₀ лежат в интервале от 18 до 27. Как видно из рис. 8.3, константа скорости при этом увеличивается от 2 (для Т-Т₀=10°С) до 5 раз (для Т -Т₀=20 °С). Максимальное увеличение k достигается только при выполнении условий адиабатичности. Возможность столь существенного изменения константы скорости не может не отразиться на форме наблюдаемых кинетических кривых. Очевидно, что эффект должен зависеть от соотношения между временем в меру (выдержкой под давлением) t и характерным временем охлаждения сжатого образца .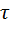

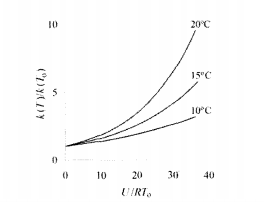
Рис. 8.3 - Зависимость константы скорости от величины активационного барьера для случая Т₀= 300 К. Изменения температуры указаны на кривых.

Охлаждение идет через стенки камеры, масса и теплоемкость которой всегда достаточно велики, чтобы считать контакт изотермическим. Скорость охлаждения (как и степень адиабатичности сжатия) определяется теплопроводимостью самого образца (скажем, воды), она конечна, и поэтому выравнивания температуры не может происходить мгновенно. С другой стороны, это означает, что процесс сжатия не может быть полностью адиабатическим и максимальный рост температуры возможно только в экспериментах со скачком давления или при использовании импульсной обработки давлением. При t<τ и Т>Т₀ cкорость реакции внутри объема образца выше, чем на периферии. При t > τ температура выравнивается, средняя по объему скорость реакции падает, что и наблюдается как новая «фаза с повышенной сопротивляемостью давления». Возможность фиксации этой фазы на опыте зависит, прежде всего, от величины изменения температуры, определяется не только величиной самого давления, так и временем его нагнетания по сравнению с τ. Кроме того, само время охлаждения τ зависит от конструкционных особенностей используемой камеры высокого давления, ее размеров, теплопроводности жидкости, передаваемого давления, упаковочного материала и тому подобного.

Согласно с [133], выравнивание температуры описывается нестационарным уравнением теплопроводности:

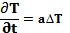, (8.4)

Где а - коэффициент теплопроводности, определяемый отношением теплопроводности 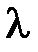с плотностью 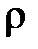и к удельной теплоемкости С, - оператор Лапласа.

В рассматриваемом случае эта задача с заданными граничными и начальными условиями. Камера высокого давления, заполненная рабочей жидкостью, представляет собой цилиндр радиуса Rc. Ограничен двумя плоскостями. Решение для этого случая, как известно, имеет вид произведений рядов за косинусами вдоль оси цилиндра и по функциям Бесселя вдоль расстояния от оси, причем скорость затухания различных гармоник возрастает с ростом их номера [134]. Грубую оценку характерного времени экспоненциального остывания для длинного цилиндра можно получить по формуле

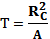(8.5)

Принимая для водной среды как для воды [135]

λ ~ 0,6 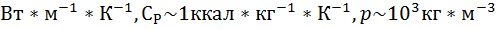в случае цилиндра радиусом 1 см получаем оценку Т ~ 10 мин, которая попадает в область характерных экспозиций (обычно от 5 до 30 мин).Таким образом, при снятии кинетической кривой исследователи неизбежно охватывают как участок t < τ, так и t > τ. Интересно отметить, что оценка времени остывания τ не зависит от увеличения нагрева.