Усреднения по объему

Для расчетов измененных кинетических кривых с учетом нестационарного распределения температуры в сжатом объеме надо переходить от точечного кинетического уравнения (1) (при n = 1) к уравнению в частных производных, которое учитывало бы диффузные потоки продуктов реакции. Однако уравнение (6.1) и (8.1) записаны для разбавленных растворов, поскольку не учитывают обратной реакции и нет нужды идти от этого приближения. Иначе говоря, пренебрежем диффузионными потоками микроорганизма между участками с разной концентрацией и округлим решение по объему сжатого образца с учетом неоднородного затухающего распределения температуры. Это распределение получается как решение уравнения теплопроводности (8.4) при заданных начальных и граничных условиях. Как правило, рабочая камера в аппаратах высокого давления имеет вид цилиндра, длина которого намного больше радиуса 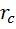. Термическое сопротивление теплоотдачи стальных стенок камеры мало, если сравнивать с внутренним сопротивлением теплопроводности жидкого образца, следовательно, можно считать, что температура внешней поверхности всегда равна начальной Т₀. Воспользуемся асимптотическим решением для бесконечного цилиндра для распределения превышение температуры над Т₀

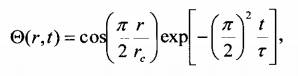(8.6)

Где Θ (r, t) - безразмерное распределение температуры в единицах максимального превышение, которое задается величиной адиабатического нагрева при сжатии βP(для воды β = 3°С/100 МПа). Таким образом, распределение температуры в образце имеет вид

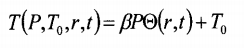(8.7)

Упрощенное решение (8.6) выбрано для приближенного моделирования последствий неравномерного охлаждения, тем не менее, при τ= 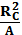оно удовлетворяет уравнению (8.4), а также предельным и начальным условиям, которые вытекают из того, как поставлена задача

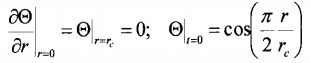(8.8)

Заметим, что начало отсчета времени t = 0 соответствует окончанию повышение давления. Этап роста давления сознательно не рассматривается, чтобы не загромождать результат техническими параметрами, которые меняются от опыта к опыту. Такое же приближения делалось раньше (тема 7) для расчета кинетических параметров без учета охлаждения.

Усредняющие результаты решения точечного кинетического уравнения первого порядка по объему образца

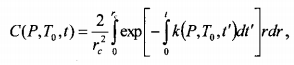(8.9)

Где константа скорости реакции определяется по формуле Арениуса с данным температурным распределением (8.7)

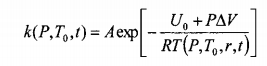(8.10)

Посмотрим, как изменятся кинетические кривые с учетом охлаждения образца после адиабатического сжатия. Для этого рассчитаем InC (Р,Т₀,t) как функцию t для случая Р = 600 МПа, Т₀= 298 К, значения других параметров были указаны выше данным обработки МАФАМ (табл. 7.1).

Результаты для разного времени охлаждения τ изображены графически на рис. 8.4. Параметр τ, как было указано выше, пропорциональный квадрату радиуса камеры R_С. И, собственно, отражает конструкционные особенности установки высокого давления, которая использовалась. Таким образом, при прочих равных условиях в камерах различного размера будут получаться разные результаты (см. Рис. 8.4). Образовавшиеся кривые по форме напоминают двухфазную или нелинейную кинетику (см. Рис. 8.1). Как видно из рис. 8.4, скорость падения In(С) при малых t ˂ τ существенно выше, чем при больших. Однако подчеркнем, этот результат получен в рамках линейной кинетики без каких-либо дополнительных предположений о составе популяции, изменение ее сопротивляемости давления и др.

Если базироваться на предложенной схеме оценок, можно рассчитать поправки к кривым в зависимости степени выживаемости от давления, которые были получены в теме 6 в пределах точечной модели первого порядка. Результаты расчетов предоставлено на рис.8.4.

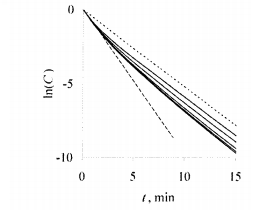
Рис.8.4 – Непрерывные линии – кинетические кривые, рассчитаны по формулам (8.6) – (8.10) для МАФАМ в вишневом соке при различных значениях времени охлаждения τ = 5, 10, 20, 30, 40 мин.(сверху вниз) для случая P = 600 Мпа, Т₀ = 278 K, пунктирные линии – кинетика без учета нагрева, штриховая линия – начальная фаза инактивации.

Пунктирные линии на рис. 8.5 соответствуют исходным кривым инактивации МАФАМ (см. Рис. 7.2) в зависимости от давления для двух значений времени обработки t = 10 и 20 мин, которые происходили при начальной температуре 25°С. Непрерывные линии - результаты расчета по формулам (8.6) - (8.10) с учетом нагрева и неравномерного охлаждения в случае τ = 10 мин.

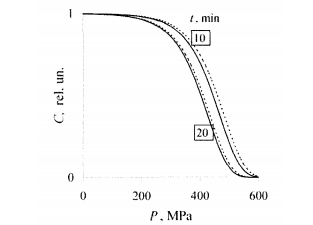
Рис.8.5 - Зависимость относительной концентрации МАФАМ в вишневом соке от давления обработки без учета (пунктир) и с учетом нагрева по формулам (8.6) - (8.10) для случая t = 10 мин, T₀= 278 К (непрерывные линии) время обработки указано на кривых

Как видно из рис.8.5, зависимости от давления качественно не изменяются. Пороговое значение давления, при котором наблюдается резкое падение концентрации, сдвигается в сторону меньших давлений на 20 и 10 МПа для t = 10 и 20 мин соответственно. С ростом времени обработки поправка на нагрев уменьшается за счет уменьшения средней температуры, при которой происходит инактивация. Таким образом, учет адиабатического нагрева не проявляет весомого влияния на результаты, полученные в теме 6.

Итак, показано [5], что отклонения от линейности могут возникать в пределах линейной модели с учетом нестационарного пространственно-неоднородного распределения температуры внутри образца. Отклонение от линейности наиболее весомые, когда время мало по сравнению с характерным временем охлаждения, которое определяется геометрией камеры сжатия. Отклонение увеличиваются с увеличением давления обработки и скорости его нагнетания.

Вероятно, такие же эффекты могут иметь место и для других процессов, как минимум, для денатурации белков под давлением, которая является причиной инактивации микроорганизмов. Основываясь на полученных результатах, можно отклонить ненужные предположения, которые обычно выполняются для объяснения особенностей кинетики этих процессов. С другой стороны, тот факт, что линейная кинетическая модель способна описать отклонения от линейности, наблюдаемых на практике, является лишним подтверждением достоверности результатов, полученных в рамках этой модели.

Вопросы для самоконтроля

1. О чем свидетельствует линейная зависимость логарифма концентрации от времени обработки или химической реакции под воздействием давления?

2. Какие причины нелинейности?

3. Почему температура образцов повышается при сжатии?

4. От чего зависит повышение температуры образцов при сжатии?

5. Как зависит повышение температуры от скорости сжатия?

Задачи и примеры

1. Рассчитать повышение температуры образцов при адиабатическом сжатии под давлением 500 мпа при уменьшении объема от 1000 до 900 мл?

2. Рассчитать разницу скорости инактивации для двух асимптот, изображенных штриховыми кривыми на рис.8.4.