Анализ возможностей модели

Задание

Предположим, что величина концентрации зависит от времени t согласно c (6.3), а также от температуры Т и давления Р по формуле (5.14). Построим выборочно эти зависимости, используя значение [1] параметров ∆V = -0,0002 еВ/МПа - для МАФАМ и ∆V = -0,00002 еВ/МПа - для витамина С (рис. 6.3). При этом в обоих случаях считаем А =3,88• 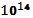, U = 1 еВ.

Как видно из рис. 6.3а, увеличение времени обработки изменяет порог полной стерилизации микроорганизмов в сторону меньшего давления. При этом концентрация витамина С равномерно снижается с ростом выдержки при любом давлении.

Увеличение температуры обработки (рис. 6.3б) также изменяет порог полной стерилизации МАФАМ в сторону меньшего давления, тогда как концентрация витамина С с ростом температуры падает ускоренно при любом давлении.

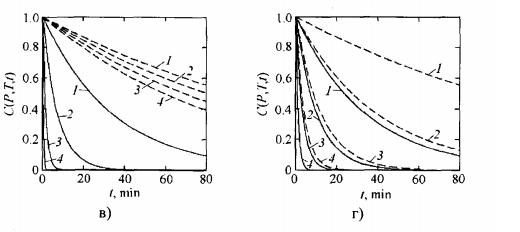
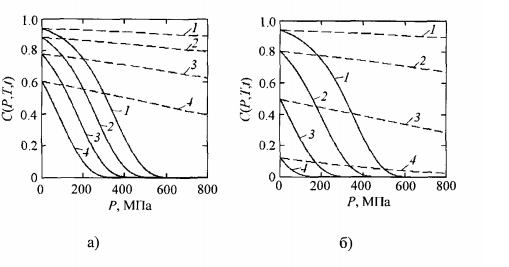
Рис.6.3-Зависимости концентрации МАФАМ (цельные линии) и витамина C (штриховые линии): а) от давления P при постоянной температуре T=300 K и разных выдержках t: 1 – 10, 2 – 20, 3 – 40, 4 – 80 мин.; б) от давления P при постоянной выдержки t=10 мин. и различных температурах T: 1 – 300, 2 – 310, 3 – 320, 4 – 330 K; в) от выдержки t при постоянной температуре T=300 K и разных давлениях P: 1 – 200, 2 – 400, 3 – 600, 4 – 800 МПа; г) от выдержки t при постоянном давлении P=200 Мпа и различных температурах T: 1 – 300, 2 – 310, 3 – 320, 4 – 330 K.

Анализ полученных кривых показывает, что влияние увеличения времени выдержки отличается от эффектов влияния и давления, и температуры. Зависимость концентрации от времени характеризуется постоянным положительным знаком второй производной, как для микроорганизмов, так и для витамина С.

Увеличение продолжительности выдержки эквивалентно росту числа попыток преодолеть активационный барьер реакции распада, в какой-то степени пропорционально количеству каналов распада. Тем самым изменение времени в определенной степени уравнивает молекулы различных размеров, имеющих различные каналы распада.

Методика обработки экспериментальных данных

Выявить роль каждого из исследованных факторов Р, Т и t довольно сложно. Для обработки и анализа экспериментальных данных можно ввести безразмерный параметр х как комбинацию факторов Р, Т и t, которые однозначно определяют величину концентрации

С = ехр [- ехр (х)], (6.4)

где

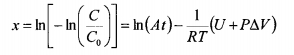(6.5)

Концентрация монотонно падает с ростом х (рис. 6.4). Сама же величина х линейно возростает с повышением давления Р, обратной температуры 1/Т и логорифма времени обработки lnt. Соответственно скорости роста величин х имеют вид:

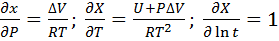(6.6)

Они существенно положительные и линейным образом связаны с неизвестными параметрами теории и U и 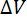, а неизвестный параметр ln(А) сдвигает х на постоянную величину. Имея достаточное количество экспериментальных точек (рис. 6.4), можно определить эти параметры методом наименьших квадратов или непосредственно из соотношений (6.5) и (6.6).

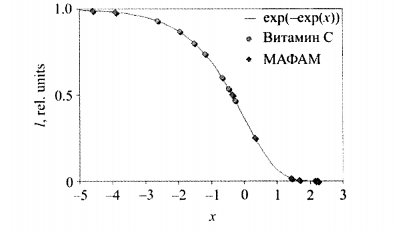
Рис. 6.4 - Положение экспериментальных точек в зависимости от безразмерного параметра х.

Как видно из (6.5), уравнение х (Р, Т, t) = соnst является уравнением плоскости в координатах Р/T, 1/Т и Int. Пересечение этой плоскости с любой из координатных плоскостей дает нам уравнение прямой линии. Неизвестные параметры теории можно получить, «выпрямляя» и анализируя экспериментальные фазовые диаграммы [2].

Задание

Записывая для каждой экспериментальной точки равенство (6.5), получаем систему с 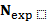линейных уравнений с тремя неизвестными ln(A),U и ∆V

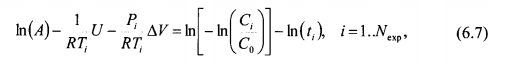
где 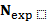- общее количество экспериментальных точек в наборе.

Переопределенную систему (6.7) можно решить методом наименьших квадратов и получить набор параметров In(А), U и ∆V, при котором теоретические кривые наилучшим образом будут проходить через все экспериментальные данные. Ценность полученного решения заключается в том, что с помощью всего лишь трех параметров можно получить реакцию системы на любое сочетание внешних воздействий давления, температуры и времени.