Интегральные уравнения пограничного слоя
Для теплового пограничного слоя уравнение энергии имеет вид:
wх 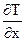 + wу
+ wу 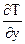 = a
= a 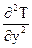
Поскольку qy = - l ¶Т/¶у и Þ l ¶Т2/¶у2 = - ¶qy/¶у Þ уравнение энергии имеет вид
rср(wх 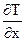 +wу
+wу 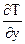 ) = - ¶qy/¶у(1)
) = - ¶qy/¶у(1)
Проинтегрируем это уравнение от у = 0 до у = ¥. Заметим, что за пределами пограничного слоя производные, входящие в уравнение (1), равны 0. Поэтому увеличение верхнего предела от k до ¥ не дает изменение интеграла.
Интегрирование правой части уравнения (1) дает
- 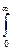
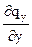 dy = qc, (плотность теплового потока на стенке)
dy = qc, (плотность теплового потока на стенке)
здесь учтено, что (qy)у=¥ = - l (¶Т/¶у) у=¥ = 0.
В результате интегрирования получим
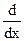
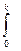 wх(T0 - T)dy = -
wх(T0 - T)dy = - 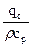 – (2)
– (2)
– интегральное уравнение теплового потока для теплового пограничного слоя
Здесь k – толщина теплового пограничного слоя;
T0 – температура невозмущенного потока.
В приближенных расчетах функциями wх = wх(у) и Т = Т(у) часто задаются исходя из опытных данных. Тогда с помощью этого уравнения можно определить, как изменяется тепловой пограничный слой вдоль оси х, то есть:
k = k(х)
Уравнение движения в проекциях на ось Ох для рассмотрим здесь течения в приближении пограничного слоя:
Wx 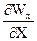 + Wу
+ Wу 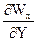 = n
= n 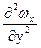 (А)
(А)
Учитывая, что касательная сила трения S = m (¶wx/¶y) и n = m/r, представим уравнение (А) в
динамический коэф.вязк. кинематич.коэф.вязкости
виде r (Wx 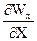 + Wу
+ Wу 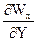 ) = ¶S/¶y(3)
) = ¶S/¶y(3)
Видим, что уравнение энергии (1) и уравнение движения (3) аналогичны. Поэтому, выполняя аналогичные преобразования над уравнением (3) получим интегральное уравнение импульсов для гидроэлектродинамического пограничного слоя
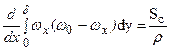 (4)
(4)
Здесь Sс – касательное напряжение трения при у = 0, то есть на поверхности стенки; d - толщина гидродинамического пограничного слоя.
Полученные уравнения пригодны и для турбулентного пограничного слоя, если под wх и Т подразумевать осредненные во времени значения скорости и температуры.
Дата добавления: 2021-09-07; просмотров: 780;











