Приведение математической формулировки краевой
задачи к записи в безразмерной форме

Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны T0 и w0 соответственно.
Предполагаем, что физические параметры жидкости постоянны (учтем только подъемную силу, возникающую в результате зависимости плотности от температуры). Рассмотрим процесс – стационарный (Т и скорость в каждой точке жидкости не изменяется). Расположим ось ОУ нормально к поверхности тела, а ось ОХ – направлена вдоль тела и вертикальна. При этом gх = g, а проекции вектора сил тяжести (или подъемной силы) на оси ОУ и OZ gy = gz = 0. Размер тела вдоль оси OZ намного больше l0.
При принятых условиях поля температур и скоростей можно описать дифференциальными уравнениями в приближении пограничного слоя:
wх (¶u/¶х) + wy (¶u/¶y) = a (¶ 2u/¶y 2 ) – уравнение энергии,
(так как толщина теплового пограничного слоя k >> l, то теплопроводностью вдоль слоя пренебрегаем, то есть ¶2u/¶х2 = 0), u = Т – Т0. движение только вдоль ОХ
wх (¶wх/¶х) + wу( ¶wх/¶у) = n (¶2w/¶у2) + gbu - уравнение движения,
сила трения подъемн. сила
*) Здесь полная скорость изменения по времени wх равна
dwx/dt = ¶wx/¶t + wх (¶wх/¶х) + wу (¶wх/¶у) + wz (¶wz/¶z)
¶wх/¶х + ¶wу/¶у = 0 – уравнение сплошности.
Граничные условия имеют вид:
 1) вдали от тела (у = ¥)
1) вдали от тела (у = ¥)
u = u0 = 0; wх = w0; wу = 0
2) на поверхности тела (у = 0, 0 £ х £ 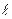 0, -¥ £ z £ +¥)
0, -¥ £ z £ +¥)
u = uс º Тс – Т0 = const; wх = wу = wz = 0
В уравнениях и условиях однозначности различают 3 вида величин:
Независимые переменные – х, у;
Зависимые переменные - u, wх, wу;
Постоянные величины - w0, T0, 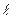 0, n, а, g, b и др. – они задаются условиями однозначности.
0, n, а, g, b и др. – они задаются условиями однозначности.
Таким образом, искомые зависимые переменные u, wх, wу зависят от большого числа величин.
Величины, содержащиеся в уравнениях и условиях однозначности, можно сгруппировать в комплексы. Число безразмерных комплексов меньше числа размерных величин.
Для привидения к безразмерному виду выберем масштабы привидения. Для линейных величин выберем какой- либо характерный размер, например, длину поверхности теплообмена l0, для скорости w0, для температуры uс.
 Обозначим безразмерные величины:
Обозначим безразмерные величины:
Х = х/ 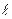 0; Y = у/
0; Y = у/ 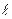 0; Wx = wх/w0;
0; Wx = wх/w0;
Wy = wy/w0; Q = u/ uс. (а)

Тогда Х 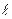 0 = х; Y
0 = х; Y 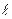 0 = у; Wxw0 = wх;
0 = у; Wxw0 = wх;
Wyw0 = wy; Quс = u. (б)
Подставим в уравнения согласно равенствам (б), получим:
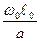 (Wx
(Wx 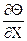 + Wy
+ Wy 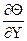 ) = ¶Q2/¶Y2 – уравнение энергии
) = ¶Q2/¶Y2 – уравнение энергии
Здесь Ре 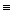 (w0
(w0 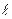 0)/а – число Пекле
0)/а – число Пекле
w0 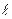 0/а =( rсрw0u)/(lu/
0/а =( rсрw0u)/(lu/  0) – здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.
0) – здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.
Дата добавления: 2021-09-07; просмотров: 654;











