Теплоотдача при турбулентном пограничном слое
Перенос теплоты и количества движения поперек турбулентного пограничного слоя можно описать уравнениями:
q = - (l + lт)× 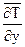 = - (l + rсрeq)×
= - (l + rсрeq)× 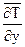 ,
,
S = (m + mт)× 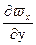 = (m + res)×
= (m + res)× 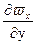 ,
,
где S – касательная сила трения; lт, mт – коэффициенты турбулентного переноса теплоты и кол-во движения; eq = lт/rср ,es = mт/r - кинематические коэффициенты турбулентного переноса теплоты и кол-ва движения.
Эти уравнения можно переписать в виде:
q = - l(1 + 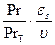 )×
)× 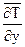 (1)
(1)
S = rn(1 + es/n)× 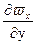 (2)
(2)
Здесь Prт = es/eq; Pr = n/а = n/l/сr
Величину Prт – называется турбулентным числом Прандтля. С учетом (1) и (2) дифференциальное уравнение энергии и движения для турбулентного пограничного слоя примут вид
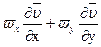 = а
= а 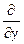 [(1 +
[(1 + 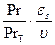 )
) 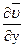 ], (3)
], (3)
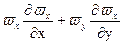 = n
= n 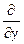 [(1 + es/n)
[(1 + es/n) 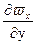 ]. (4)
]. (4)
Если Pr = 1 (а = n) и Prт = 1, то уравнения (3) и (4) идентичны. В этом случае при идентичных граничных условиях поля температуры u и скорости vх будут подобны.
Для того, чтобы проинтегрировать уравнение (3) и (4), необходимо иметь сведения о коэффициентах турбулентного переноса теплоты es и eq.
Опыты показывают сложность движения в турбулентном слое:
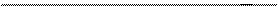
 А А
 d
d
   Б
II Б
II
               dп I dп I
| Рис. Турбулентный пограничный слой А – внешняя область; Б – пристенная область (I – вязкий подслой (ламинарный); II – промежуточный слой). Пульсации, особенно крупномасштабные (низкочастотные), проникают в вязкий подслой, где их течение регламентируется |
вязкими силами. Поэтому граница подслоя четко не определена. Наиболее высокая интенсивность турбулентности наблюдается в пристенной области Б. Внешняя граница турбулентного пограничного слоя непрерывно пульсирует. В зависимости от области характер переноса теплоты различен.
Аналогично вязкому подслою непосредственно у стенки наблюдается тепловой подслой.
Он характеризуется преобладанием теплоты теплопроводностью над турбулентным переносом.
При Pr = 1 толщина вязкого подслоя dп и теплового kп совпадают.
Поскольку в тепловом подслое перенос теплоты определяется теплопроводностью, то изменение температуры по его толщине описывается уравнением прямой (как для плоской стенки). В остальной части турбулентного слоя температура распределяется по логарифмическому закону.
Зная распределение скоростей и температуры, можно рассчитать теплоотдачу с помощью интегральных уравнений теплового потока и импульса.
Дата добавления: 2021-09-07; просмотров: 655;











