Теплоотдача при ламинарном пограничном слое

Для расчета теплоотдачи при ламинарном слое используем интегральное уравнение теплового потока для теплового пограничного слоя:

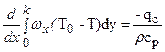
Чтобы рассчитать теплоотдачу, необходимо знать распределение скорости в слое. В случае ламинарного пограничного слоя распределение скорости в нем близко к параболе (кубическая парабола):

w_х = а + bу + су² + dу³(a)

Уравнение распределения скорости должно удовлетворять граничным условиям.

При у = 0 w_х = 0 (условие «прилипания»), полагаем также, что (¶²w_х/¶у²) = 0.

При у = d (на внешней границе слоя) w₀ = w_х и (¶w_х/¶у) = 0.

Уравнение (а) будет удовлетворять этим требованиям, если

а = 0; с = 0;b = 3/2w₀/d; d = - 1/2w₀/d³.

Распределение скорости при этом примет вид:

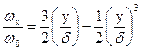(б)

При распределении скорости согласно (б) из интегрального уравнения импульсов

-

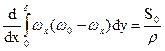можно получить, что толщина гидродинамического пограничного слоя определяется выражением:

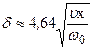
или в безразмерной форме

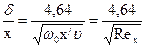
Таким образом, толщина d изменяется пропорционально корню квадратному из расстояния от переднего края пластины до данной точки. Чем больше вязкость, тем толще d. Чем выше скорость – тем меньше (тоньше) слой d.

Пограничные условия для температур:

При у = 0 u (здесь и ниже принято u = Т – Тс) и (¶u/¶у)_у=0 = const и Þ (¶²u/¶у²) = 0, если учесть, что в жидкости, непосредственно прилегающей к плоской стенке, теплота передается по у только теплопроводностью.

При у = k (на внешней границе теплового слоя) u = u₀ = const и (¶u/¶у)_у=k = 0.

То есть граничные условия получились аналогичны принятым ранее условиям для гидродинамического пограничного слоя.

В результате получаем, что распределение температуры описывается уравнением, аналогичным по форме записи уравнению распределения скорости

u/u₀ = 1,5 (у/k) – 0,5 (у/k)³ (А)

После подстановки в интегральное уравнение теплового потока и упрощений получили:

,

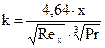где Re_х = w₀х/n; Рr = n/а.

Тогда 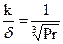– то есть отношение k/d не зависит от х, а зависит только от числа Рr.

Для капельных жидкостей Рr ³ 1, Þd³ k.

Для газов Рr = 0,6 – 1 (для воздуха Рr » 0,7). При этомk>d.

Определим коэффициент теплоотдачи из уравнения 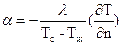, Þ 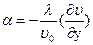_у=0 зная, что 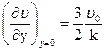(это следует из производной), опуская знак ²-² получим:

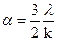(а)

Коэффициент теплоотдачи обратно пропорционален толщине пограничного слоя (чем меньше толщина k, тем больше a Þ лучше теплоотдачи).

Уравнение (а) можно привести к безразмерному виду (умножив левую и правую части на х/l и подставляя значение ):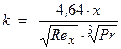

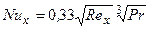(б)

Здесь Nu_x = ax/l = a 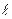/l x/ 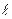= Nu_еX; Re_x = w₀x/n = w₀ 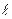/n x/ 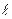= Re_еX; Pr = n/a; 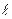– длина пластины вдоль потока.

Формула (б) справедлива только при условии, что температура поверхности пластины постоянна, физические параметры жидкости не зависят от температуры и в начале пластины нет необогреваемого участка.

Коэффициент теплоотдачи капельной жидкости зависит от рода жидкости, ее температуры, направления теплового потока. Особенно существенное влияние оказывает зависимость вязкости от температуры. При охлаждении жидкости, вязкость увеличивается, течение замедляется. Поэтому для жидкостей вводится поправка (Pr_ж/ Pr_с)^0,25, которая учитывает влияние на теплообмен изменения вязкости. Для (Pr_ж/ Pr_с)^0,25 Þ 1.

Индекс «с» - означает, что Pr_с вычислен при температуре стенки; «ж» - при температуре жидкости вдали от стенки.