При параллельном переносе осей
|
Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.
ТеоремаМомент инерции относительно какой-либо оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.
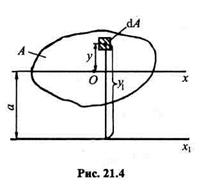
Пусть дана произвольная плоская фигура, площадь которой А,центр тяжести расположен в точке С, а центральный момент инерции относительно оси х будет Ix. Вычислим момент инерции фигуры относительно оси x1, параллельной центральной и отстоящей от нее на расстоянии а (рис. 21.4):
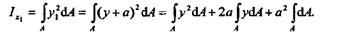
Первое слагаемое правой части есть момент инерции фигуры относительно оси х,т. е. Ix; второе слагаемое содержит статический момент площади относительно оси х, а он равен нулю, так как ось х — центральная; третье слагаемое после интегрирования будет равно а2А. Врезультате получим
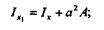
теорема доказана.
Нужно помнить то обстоятельство, что последней формулой можно пользоваться только в тех случаях, когда одна из параллельных осей — центральная.
Анализируя выведенную формулу, можно сделать вывод, что из ряда параллельных осей момент инерции будет наименьшим относительно центральной оси.
Пользуясь доказанной теоремой, выведем формулу для вычисления момента инерции прямоугольника относительно оси x1, проходящей через основание (см. рис. 21.3):
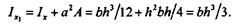
Дата добавления: 2021-09-07; просмотров: 437;











