Закон парности касательных напряжений

Закон парности касательных напряжений форму­лируется так: касательные напряжения в двух взаимно перпендикулярных площадках, перпендикулярные их общему ребру, равны по модулю.

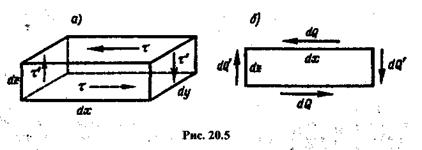
Внутри тела вблизи некоторой точки вырежем элементарный парал­лелепипед с размерами dx, dy, dz (рис. 20.5, а).

Пусть на верхней грани этого параллелепипеда действует касатель­ное напряжение т. Сила, действующая в этой грани, равна

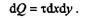
Так как параллелепипед находится внутри тела в равновесии, то 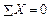, следовательно, на нижней грани параллелепипеда будет дейст­вовать такая же сила dQ, но направленная в противоположную сторону. Пара сил (dQ, dQ) будет стремиться вращать параллелепипед против ча­совой стрелки (рис. 20.5, б).

Так как параллелепипед находится в равновесии, то 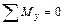, сле­довательно, пара (dQ, dQ) будет уравновешиваться какой-то другой парой с моментом, равным моменту первой пары. Естественно считать, что вто­рая пара образуется касательными напряжениями 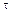', действующими на боковых (правой и левой) гранях параллелепипеда, причем dQ' = 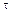'dydz. Следовательно,

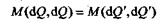
или

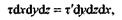
откуда

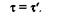
Обратим внимание на то, что парные касательные напряжения в двух взаимно перпендикулярных сечениях направлены либо к линии пересече­ния плоскостей сечений, либо от этой линии.