Деформация и закон Гука при сдвиге
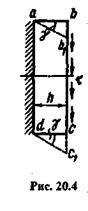
Для установления параметров, характеризующих деформацию при сдвиге, рассмотрим элемент бруса в виде параллелепипеда abсd,на грани которого действуют только касательные напряжения 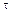 , а противоположную грань параллелепипеда представим жестко защемленной (рис. 20.4). Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bс по отношению к сечению, принятому за неподвижное. Деформация сдвига характеризуется углом
, а противоположную грань параллелепипеда представим жестко защемленной (рис. 20.4). Деформация сдвига в указанном элементе заключается в перекашивании прямых углов параллелепипеда за счет поступательного перемещения грани bс по отношению к сечению, принятому за неподвижное. Деформация сдвига характеризуется углом 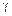 и называется углом сдвига или относительным сдвигом (так как этот параметр не зависит от
и называется углом сдвига или относительным сдвигом (так как этот параметр не зависит от
|
расстояния h,на котором происходит сдвиг). Величина bb1, на которую смещается подвижная грань относительно неподвижной, называется абсолютным сдвигом. Относительный сдвиг 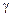 выражается в радианах.
выражается в радианах.
Напряжения и деформации при сдвиге связаны между собой зависимостью, которая называется законом Гука при сдвиге.
Закон Гука при сдвиге справедлив лишь в определенных пределах нагружения и формулируется так: касательное напряжение прямо пропорционально относительному сдвигу.
Математически закон Гука можно записать в виде равенства
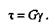
Коэффициент пропорциональности G характеризует жесткость материала (т. е. способность сопротивляться упругим деформациям) при сдвиге и называется м о д у л е м сдвига или модулем упругости второго рода.
Модуль упругости и напряжение выражаются в одинаковых единицах:
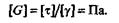
|
Значения G, МПа, для некоторых материалов:
Чугун........................................................ 4,5  104
104
Сталь........................................................ 8,1  104
104
Медь................................. ………………....(4,0...4,9)  104
104
Латунь..................................................... (3,5...3,7)  104
104
Алюминий .................................................. (2,6...2,7)  104
104
Дерево...................................................... 0,055  104
104
В заключение отметим, что между тремя упругими постоянными Е, G и v существует следующая зависимость:

Принимая для сталей v 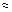 0,25, получаем
0,25, получаем
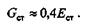
Дата добавления: 2021-09-07; просмотров: 474;











