Теорема об изменении количества движения
Общие теоремы динамики материальной точки устанавливают зависимость между изменением динамических мер движения материальной точки и мерами действия сил, приложенных к этой точке.
Количеством движения тvматериальной точки называется вектор, равный произведению массы точки на ее скорость и имеющий направление скорости. Количество движения есть динамическая мера движения материальной точки.
Единица количества движения
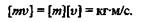
Импульсом Ft постоянной силы F называется вектор, равный произведению силы на время ее действия. Импульс силы есть мера ее действия во времени.
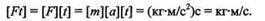
|
| Единица импульса силы |
Количество движения и импульс силы выражаются в одинаковых единицах, связь между ними устанавливает теорема об изменении количества движения,формулируемая так: изменение количества движения материальной точки за некоторый промежуток времени равно импульсу приложенной к ней силы за тот же промежуток времени.
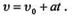
|
Перенесем 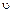 oв левую часть и умножим обе части равенства на массу т материальной точки: oв левую часть и умножим обе части равенства на массу т материальной точки:
|
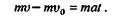
|
| Но произведение массы точки на ее ускорение есть сила, под действием которой точка движется; следовательно, |
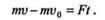
|
Докажем эту теорему для случая прямолинейного движения материальной точки под действием постоянной силы F, в этом случае движение будет равнопеременным, формула скорости которого записывается так:
В левой части равенства имеем изменение количества движения за время t, а в правой — импульс силы за тот же промежуток времени, что и требовалось доказать.
Если движение замедленное ( 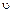 <
<  0), то вектор силы направлен в сторону, противоположную вектору скорости, и, следовательно, в последнюю формулу силу надо подставлять с отрицательным знаком.
0), то вектор силы направлен в сторону, противоположную вектору скорости, и, следовательно, в последнюю формулу силу надо подставлять с отрицательным знаком.
В случае криволинейного движения материальной точки под действием переменной по модулю и направлению силы весь промежуток времени t можно разбить на бесконечно малые промежутки, в пределах которых вектор силы можно считать постоянным, а путь — прямолинейным, тогда импульс силы за конечный промежуток времени t будет равен сумме элементарных импульсов. В этом случае математическое выражение теоремы об изменении количества движения приобретает следующий вид:
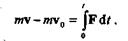
Если к материальной точке приложено несколько постоянных сил, то изменение количества движения будет равно сумме (алгебраической, если силы действуют по одной прямой, или векторной, если силы действуют под углом друг к другу) импульсов данных сил:
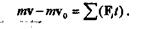
|
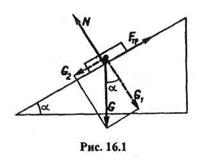
Пример 16.1. Тело спускается без начальной скорости по наклонной плоскости, составляющей с горизонтом угол  = 30° (рис. 16.1). Определить время t,в течение которого скорость движения тела достигнет 13,9 м/с. Коэффициент трения скольжения
= 30° (рис. 16.1). Определить время t,в течение которого скорость движения тела достигнет 13,9 м/с. Коэффициент трения скольжения
f = 0,25.
Решение. Рассмотрим тело как материальную точку, движущуюся под действием силы тяжести G, силы трения Fтр, и нормальной реакции N наклонной плоскости. Разложим силу тяжести G на составляющие G1 и G2, одна из которых перпендикулярна, а другая параллельна наклонной плоскости, и применим теорему об изменении количества движения:
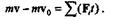
Спроецируем это векторное равенство на направление наклонной плоскости, в результате чего получим
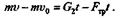
Применив второй закон трения скольжения и подставив значения, получим
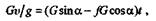
откуда
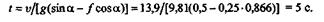
Дата добавления: 2021-09-07; просмотров: 484;











